PELL DİZİSİ PELL SAYILARI VE GÜMÜŞ ORAN
Bu yazıda Pell dizisinin tanımından hareketle; Pell sayılarını belirleyip, gümüş oran kavramını ifade edeceğiz. Ayrıca Pell dizisine ait karakteristik denklem ve üreteç matrisi kavramlarını açıklayacağız. Böylece cebirsel işlemler ve matrisleri kullanarak Pell sayılarına ait çeşitli özellikler elde edeceğiz.
Tanım: için , başlangıç koşullarıyla birlikte,
yineleme bağıntısıyla tanımlanan diziye Pell dizisi denir.
Bu dizinin elemanları Pell sayıları olarak isimlendirilir ve , sıradaki Pell sayısına karşılık gelir. O halde dizinin elemanlarını belirleyip, Pell sayılarını sıralı biçimde yazabiliriz:

Şimdi hesaplar için excel programını kullanarak ardışık Pell sayılarının birbirine bölümünden elde edilen oranları göz önüne alalım:
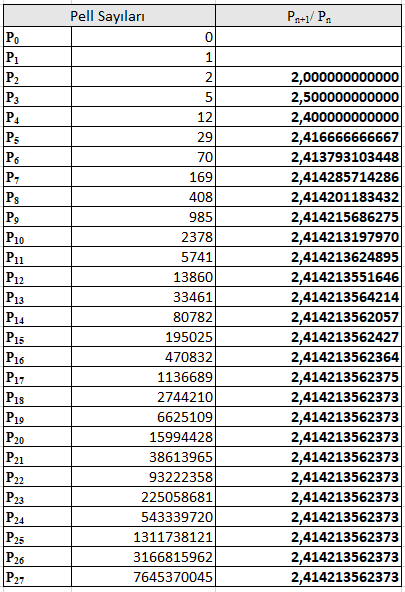
Tabloda elde edilen ardışık sayılar arasındaki oranlar dikkate alınırsa bu oranın civarı bir sayıya yakınsadığı bariz biçimde görülmektedir. İşte bu oran n sonsuz büyürken, yani limitinin yakınsadığı değer "gümüş oran" olarak isimlendirilir. O halde bu sayıyı cebirsel yaklaşımla belirlemeye çalışalım.
Dizisinin indirgeme bağıntısını ele alalım. Eşitliğin her iki tarafını ifadesine bölelim:
Sadeleşme işlemi yapılırsa
olur. işlemlerde kolaylık olması bakımından yerine yazalım. Bu durumda
eşitliği elde edilir. Eşitliğin her iki tarafını için limitini alalım
olur. Limit değerini olarak isimlendirelim,
eşitliğin her iki tarafı ile çarpılarak genişletilirse
eşitliğine ulaşılır. Tüm ifadeler sol tarafta toplanırsa
ikinci dereceden denklemi elde edilir. Denklemin diskriminant değeri ve kökler çarpımı olduğu için köklerden biri negatif diğeri pozitif olmalıdır. Öyleyse bu denklemin pozitif kökü aradığımız sayı olacaktır. kökleri bulmak için tam kareye tamamlama yöntemini kullanalım. Denklemin sol tarafında yerine yazalım:
tamkare ifadeyi derleyelim
eşitliğin sol tarafına iki kare farkı açılımıyla çarpanlara ayıralım: soldaki çarpan sıfıra eşitlendiğinde elde edilen:
pozitif kökü, aradığımız sayı olacaktır. Böylece gümüş oranın sayısal değeri, olarak belirlenir. Euclid tarafından altın oran için ifade edilen doğru parçası problemine benzer şekilde, gümüş oranın geometrik yaklaşımla elde edilmesi, aşağıda hazırladığım videoda gösterilmiştir.Bu kısımda Pell sayıları için kapalı bir formül bulacağız. Böylece sıradaki Pell sayısını hemen hesaplayabileceğiz. Aslında
eşitliğini kullanarak tüm elemanları bulabiliriz, fakat bu yöntem elemanların indisi büyüdükçe uğraşmamız gereken aritmetik işlemler giderek artacağından dolayı epey meşakkatli olacaktır. İstediğimiz formülü elde etmek için biçimsel kuvvet serilerini kullanacağız. tanımını yapalım, şimdi ifade ettiğimiz indirgeme bağıntısının her iki tarafını da tanımı uygulayarak hesaplara başlayalım. eşitliği cinsinden düzenleyip yazalım buradan sırasıyla, ve elde edilir. Payda kısmındaki polinomunun iki tane kökü vardır. Bunlarıve
şeklinde yazalım. Bu durumda şeklinde ifade edebiliriz. Bu düzenlemeyle birlikte aşağıdaki işlemler yapılırsa:polinomdan ve değerlerini yerlerine yazalım:
sonucuna ulaşılır. Böylece, olur. ile pay kısmını çarpalım son olarak ve olduğundan, şeklinde kapalı formül elde edilir. Böylece istediğimiz Pell sayısını bulmak için yerine sıra numarasını yazmak yeterli olacaktır. Şimdi hesaplama aracı yardımıyla sıra sayısına göre Pell sayılarını dinamik biçimde hesaplayalım.
Yukarıdaki uygulama sıra numarası büyüdükçe kapalı formül üzerinden sonuca ulaşmak kolay olmayacağından epey yararlı olacaktır.
Bilal DEMİR Matematik Öğretmeni