Función Logarítmica
Definición:
En análisis matemático, usualmente, el logaritmo de un número real positivo —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Gráfica de Logaritmo
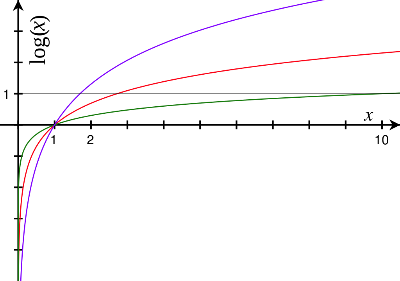
Vídeo de Logaritmo
Cuestionario
¿Cuál es el punto por el cual pasan todas las funciones logarítmicas?
¿Qué es un Logaritmo?