Curvas
Definición
Una función vectorial r(t) es un mapeo de su dominio a su rango , de modo que para cada t en D, r(t) = v para exactamente un vector . Podemos siempre escribe una función con valores vectoriales como r(t) = f(t)i + g(t)j + h(t)k, para algunas funciones escalares f, g y h (llamadas funciones componentes de r).
Ejercicios a realizar:

Ejercicio 1
Ejercicio 3
Ejercicio 5
Ejercicio 7
Ejercicio 9
Ejercicio 11
Ejercicio 13
Ejercicio 15
Ejercicio 17
Ejercicio 19
Ejercicio 21
Ejercicio 23
Ejercicio 25 inciso "a"
Ejercicio 25 inciso b
ejercicio 25 inciso c
Gráfica 6 relacionada con el inciso "a" (Ejercicio 27)
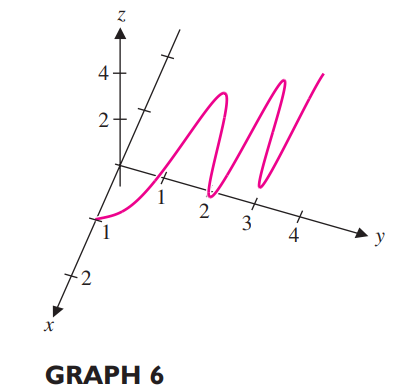
Ejercicio 27 inciso "a", se relaciona con la gráfica 6.
Gráfica 3, su parecido es con el inciso "b"

Ejercicio 27 inciso "b", se relaciona con la gráfica 3.
Gráfica 5, relaciona con el inciso "c".
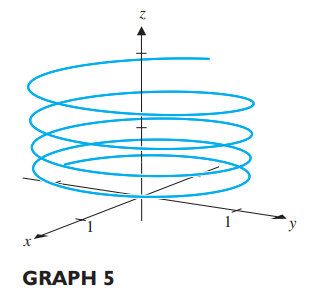
Ejercicio 27 inciso "c", se relaciona con la gráfica 5.
Gráfica 1, se relaciona con el inciso "d".
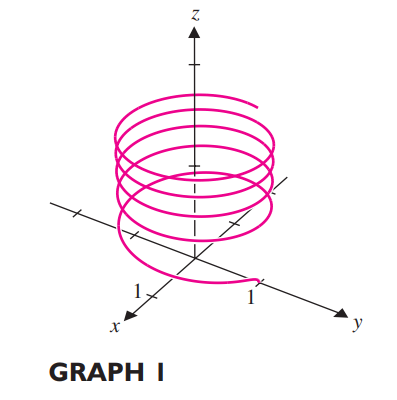
Ejercicio 27 inciso "d", se relaciona con la gráfica 1.
Gráfica 2, se relaciona con el inciso "e".

Ejercicio 27 inciso "e", se relaciona con la gráfica 2.
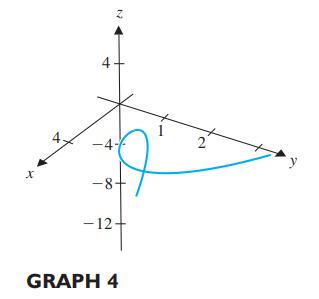
Gráfica 4, se relaciona con el inciso "f".