もっとある特殊な関数・多項式
チェビシェフ多項式
1。チェビシェフ多項式
このワークシートはMath by Codeの一部です。
前回まで、微分方程式の解法を通して、ルジャンドルとか、ベッセルとか、
特殊な関数、多項式に触れてきた。
今回は、他にもある特殊な関数、多項式をみてみよう。
<チェビシェフの微分方程式>
p(x)=1-x2,q(x)=-x , r(x)=n2 はx=0で解析的で、(1−x2)y′′−xy′+n2y=0を
チェビシェフの微分方程式という。x=0は正則点。
・級数解y=Σamxm=a0+a1x+a2x2+a3x3....(a0≠0, m for 0 to ∞)を入れてみよう。
y'=a1+2a2x1+3a3x2+......
y"=2*1a2+3*2 a3x + ...
p(x)=1-x2
q(x)=-x
r(x)=+n2
2*1a2+3*2 a3x + ...+(k+2)(k+1) ak+2xk +.....
-(2*1a2x2+3*2a3x3 ...+k*(k-1) akxk .......)
-(a1x+2a2x2+3a3x3+......kakxk+.......)
+n2(a0+a1x+a2x2+a3x3....+akxk......)=0
x0係数の和は、2a2+n2a0=0 a2=(0-n2)/2*1 a0
x1係数の和は、3*2 a3 -1a1 +n2a1=0 a3 =(1-n2)/3*2 a1
x2の係数の和は、4*3 a4 -2a2-2*1a2 +n2a2 =0 a4 =(22-n2)/4*3 a2
x3の係数の和は、5*4a5 -3a3-3*2a3 +n2a3 =0 5*4 a5 -(3+3*2-n2)a3 =0 a5 =(32-n2)/5*4 a1
xkの係数の和は、(k+2)(k+1) ak+2 -kak-k(k-1)ak +n2ak = (k+2)(k+1)ak+2 -(k+k2-k-n2)ak =0
これから、a0から始めると、
・a_even=
a1から始めると、
・a_odd =
これこら、一般解はy=a0y0(x)+a1y1(x)で、
y0(x)=1+(-n2)/2! x2+(-n2)(22-n2)/4! x4+(-n2)(22-n2)(42-n2)/6! x6+...........
y1(x)=x+(1-n2)/3! x3+(1-n2)(32-n2)/5! x5+(1-n2)(32-n2)(52-n2)/7! x7+...........
<チェビシェフの多項式>
・(1−x2)y′′−xy′+n2y=0 の第一のチェビシェフの多項式Tn(x)は、nの偶奇で式を変える。
n=2s(偶数)のとき、Tn(x)=(-1)sy0(x)、奇数n=2s+1のとき、Tn(x)= (-1)s n y1(x)。
漸化式の のn=kになったとき、k+2番目以降は0になる。
だから、Tn(x)はn次式になる。
T0(x)= 1,
T1(x)= x,
T2(x)= -(1-2x2)= 2x2-1,
T3(x)= -3(x+(1-9)/6x3)= 4x3 -3x
T4(x)= (-1)2(1-42/2! x2+(-42)(22-42)/4! x4)=1-8x2+8x4 =8x4 -8x2 +1
............
チェビシェフの多項式が面白いのは、x=cos θを代入すると、cos n θを表すn倍角の公式になることだ。
T0(cos θ)= 1 = cos0θ,
T1(cos θ)= cos θ = cos 1θ,
T2(cos θ)= 2(cos θ)2-1=cos 2θ
T3(cos θ)= 4(cos θ)3 -3(cos θ)=cos 3θ
T4(cos θ)=8(cos θ)4 -8(cos θ)2 +1 = cos 4θ
.............
Tn(cos θ)= cos nθ
cos θ=x ( θ= arccos x)を代入するともとに戻るので、Tn(x)=cos(n θ) = cos(n arccos x)
<フロベニウス法>
一般解を級数解y=Σamxm+r=xr(a0+a1x+a2x2+a3x3....)(a0≠0, m for 0 to ∞)を入れてみよう。
として、 xr−2 の係数 r(r−1)a0=0から、決定方程式の解がr=0,1となります。
だから、r=0としたものが上記の解と多項式だとわかります。
もしr=1にすると、上と同様な計算によって、漸化式ak+2=[(k+1)2−n2]/(k+3)(k+2)ak
が得られてこれを累積して係数を作ればy0(x),y1(x)ができるね。
nに偶数、奇数で分けて同様のロジックで計算していくと
第2種チェビシェフの多項式Un(x)ができるのです。
U0(x)= 1,
U1(x)= 2x,
U2(x)= 4x2-1,
U3(x)= 8x3 -4x
....................第2チェビシェフの多項式にも、x=cos θを代入してみよう。
U0(cos θ)= 1 ,
U1(cos θ)= 2cos θ ,
U2(cos θ)= 4(cos θ)2-1
U3(cos θ)= 8(cos θ)3 -4(cos θ)
かんたんな式ではありませんが、Un(cosθ)=sin((n+1)θ)/ sinθになります。
だから、cos θ=x ( θ= arccos x)を代入するとUn(x)=sin((n+1) arccos x)/√(1- x2)
2.チェビシェフ多項式の別の入り口
<ド・モアブル定理から>
チェビシェフ多項式は、別の入り口からも手に入る。
まず、ド・モアブル定理(cosθ+i sinθ) n=cos n θ+i sin n θ
これは、文字列として見るのではなく、オイラー等式からcosθ+i sinθ=eiθ
と考えれば、θの回転をn回やれば、到達する複素数はn倍のθの複素数になるので、当然だね。
また、2項定理(a + b)n=Σ nCk akbn-k [k for 0 to n]
から、(cosθ+i sinθ) n=Σ nCk cosθk(i sinθ)n-k
= cosnθ+ i cos n-1θsin1θ - cos n-2θsin2θ - i cos n-3θsin3θ + cos n-4θsin4θ + i - -i + .......
=( cosnθ- cos n-2θsin2θ + cos n-4θsin4θ - cos n-6θsin6θ +- .........)
+i(cos n-1θsin1θ - cos n-3θsin3θ + cos n-5θsin5θ - cos n-7θsin7θ +-...........)
以上から、
cos nθ= cosnθ- cos n-2θsin2θ + cos n-4θsin4θ - cos n-6θsin6θ +- .........
sin nθ= cos n-1θsin1θ - cos n-3θsin3θ + cos n-5θsin5θ - cos n-7θsin7θ +-...........だから、
sin (n+1)θ= cos nθsin1θ - cos n-2θsin3θ + cos n-4θsin5θ - cos n-6θsin7θ +-...........
となるね。
ここで、cos θ=xとして、
(cosθ+i sinθ) n=cos n θ+i sin n θの実部cosnθ=xの式=Tn(x)とし、
(cosθ+i sinθ) n+1=cos (n+1)θ+i sin (n+1)θの虚部sin(n+1)θ=sinθ(xの式)のxの式をUn(x)とする。
こういうTn(x),Un(x)を第1、第2のチェビシェフの多項式と決めることができる。
3.エルミート多項式
<微分方程式>
p(x)=-2x,q(x)=2α はx=0で解析的で、y′′−2xy′+2ky=0を
エルミートの微分方程式という。x=0は正則点。
・級数解y=Σamxm=a0+a1x+a2x2+a3x3....(a0≠0, m for 0 to ∞)を入れてみよう。
y'=a1+2a2x1+3a3x2+......
y"=2*1a2+3*2 a3x + ...
p(x)=-2x
q(x)=2α
2*1a2+3*2 a3x + ...+(k+2)(k+1) ak+2xk +.....
-(2a1x+4a2x2+6a3x3+......2k akxk+.......)
+2α(a0+a1x+a2x2+a3x3....+akxk......)=0
x0係数の和は、2a2+2αa0=0 a2=2(0-α)/2*1a0
x1係数の和は、3*2 a3 -2a1 +2αa1=0 a3 =2(1-α)/ 3*2a1
x2の係数の和は、4*3 a4 -4a2 +2αa2 =0 a4 =2(2-α)/ 4*3a2
x3の係数の和は、5*4a5 -6a3+2αa3 =0 a5 =2(3 -α)/5*4 a3
xkの係数の和は、(k+2)(k+1) ak+2 -2kak +2α ak = (k+2)(k+1)ak+2 -2(k -α)ak =0
a_even= ,
a_odd=
y=a0y0(x) + a1y1(x)が一般解。
y0(0)=Σ [s for 0 to ∞]
y1(0)=Σ [s for 0 to ∞]
・αが偶数2nのときは、a0=1, a1=0とすると、y=y0(x)となるね。
漸化式 の分子の因数k-αのために、
k=α次の係数のあとはすべて0になるから、2n次の多項式になる。
・αが奇数2n+1のときも同様にして、y=y1(x)となり、2n+1次の多項式になる。
これらがエルミート多項式だ。
<多項式>
最高次xkの係数が2kになるとしたら、
・最高次数k=α=2nのときに、その係数が22nになる。
漸化式の最後の分子は(2n-2- 2n),分母は2n*(2n-1)となるから、
ここで、2重階乗マーク!!は、1飛ばしで連続奇数の積を表すね。
・最高次数k=α=2n+1のときも同様にして、a1=(-1)n2n+1(2n+1)!!
とする。
このとき、Hn(x)=a0 y0(x)+a1y1(x)をエルミート多項式という。
a0=(-1)n(2n-1)!!, a1=(-1)n2n+1(2n+1)!!
H0(x)=a0=(-2)0(2*0-1)!!=1
H1(x)=a1x=(-1)020+1(2*0+1)!!x=2x
H2(x)=(-2)1(2*1-1)!!(1+2*(-2)/2!x2)=4x2-2
H3(x)=(-1)121+1(2*1+1)!!(1x+2(1-3)/ 3*2 x3) =-12(1x -2/3x3)=8x3 -12x
...................
エルミート多項式にも、微分形式のものがありますね。
Hn(x)=(-1)nexp(x2) (exp(-x2))(n)
3。実装
質問:チェビシェフの多項式やエルミート多項式をグラフ表示するコードはどうすれば作れますか。
特殊関数ということで、ベッセル関数と同様にscipy.specialからインポートできますね。
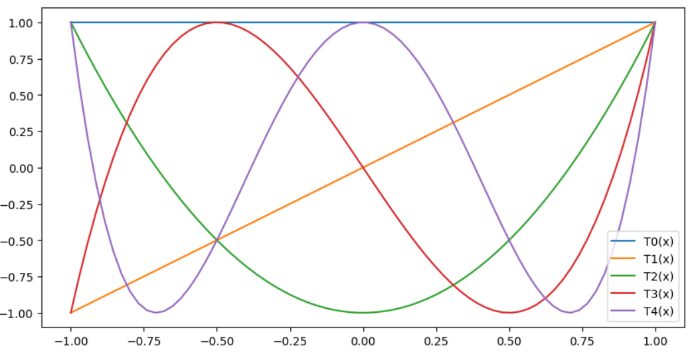
チェビシェフ第1多項式はTn(x)=eval_chebyt(n,x)でえられます。
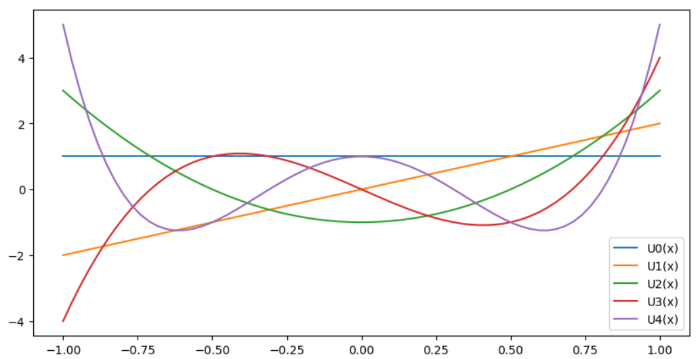
チェビシェフ第2多項式はUn(x)=eval_chebyu(n,x)でえられます。
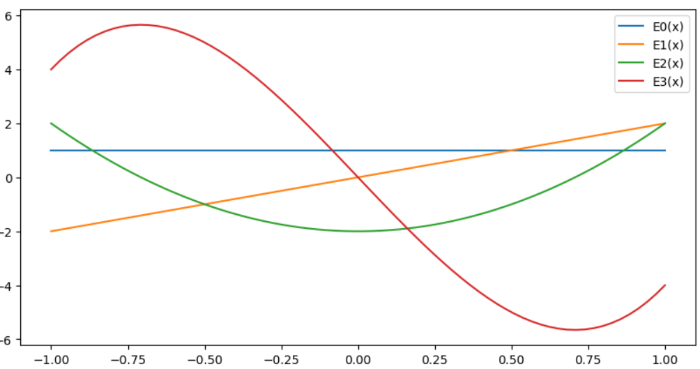
エルミート多項式はEn(x)=eval_hermite(n,x)でえられます。
x = np.linspace(-1, 1, 70)とすることで、xが-1から1の間で計算しました。
# チェビシェフ多項式
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_chebyt
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
x = np.linspace(-1, 1, 70)
for n in range(5):
ax.plot(x, eval_chebyt(n, x), label=f"T{n}(x)")
ax.legend()
# チェビシェフ多項式第2
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_chebyu
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
x = np.linspace(-1, 1, 70)
for n in range(5):
ax.plot(x, eval_chebyu(n, x), label=f"U{n}(x)")
ax.legend()
# エルミート多項式
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_hermite
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
x = np.linspace(-1, 1, 70)
for n in range(4):
ax.plot(x, eval_hermite(n, x), label=f"E{n}(x)")
ax.legend()