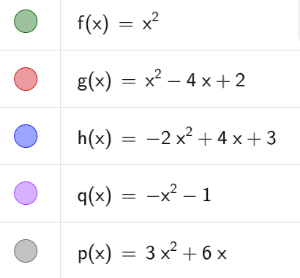Funciones 3º ESO
1º Sesión - ¿Qué es una función?
Vamos a ver algunos ejemplos de relaciones para ver si llegamos a la definición de función
- Nombre --> número de letras
- Número --> su doble
- Persona --> deporte que practica
¿Qué relación hay entre el valor de entrada y el de salida? ¿Cuál depende de cuál? ¿Cómo podríamos llamar a cada una de las variables?
¿Podríamos expresar las funciones anteriores con ecuaciones?
Pero entonces... ¿ecuación y función es lo mismo?
- ¿Cómo escribimos con una ecuación la función del número de letras de un nombre?
- ¿Y si os digo esta ecuación: ? ¿Es una función?
Y ya para ir cerrando, si tenemos la función :
- ¿Qué valores puedo meter en la x?
- ¿Y qué valores puede salir?
¡Para mañana!
Dada la siguiente situación: un parking cobra 1 € por entrar y 2 € por cada hora que estás
- Justificar por qué esta relación es una función
- Representarla con una ecuación
- Haced una tabla de valores
- Representar la gráfica
2º Sesión - Funciones lineales
Dada la siguiente situación: un parking cobra 1€ por entrar y 2 € por cada hora que estás
- Justificar por qué esta relación es una función
- Representarla con una ecuación
- Haced una tabla de valores
- Representar la gráfica
Este tipo de funciones ¿En qué tipos de sistemas las representabais?
¿Cómo se llamaban y por qué?
FUNCIONES LINEALES
Como veis, las funciones lineales las podemos representar de 4 formas:
- Verbal
- Algebraica
- Tabular
- Gráfica
Vamos a ver una cuantas funciones lineales representadas gráficamente y con sus expresiones algebraicas ¿Qué observáis? ¿Qué tienen en común?
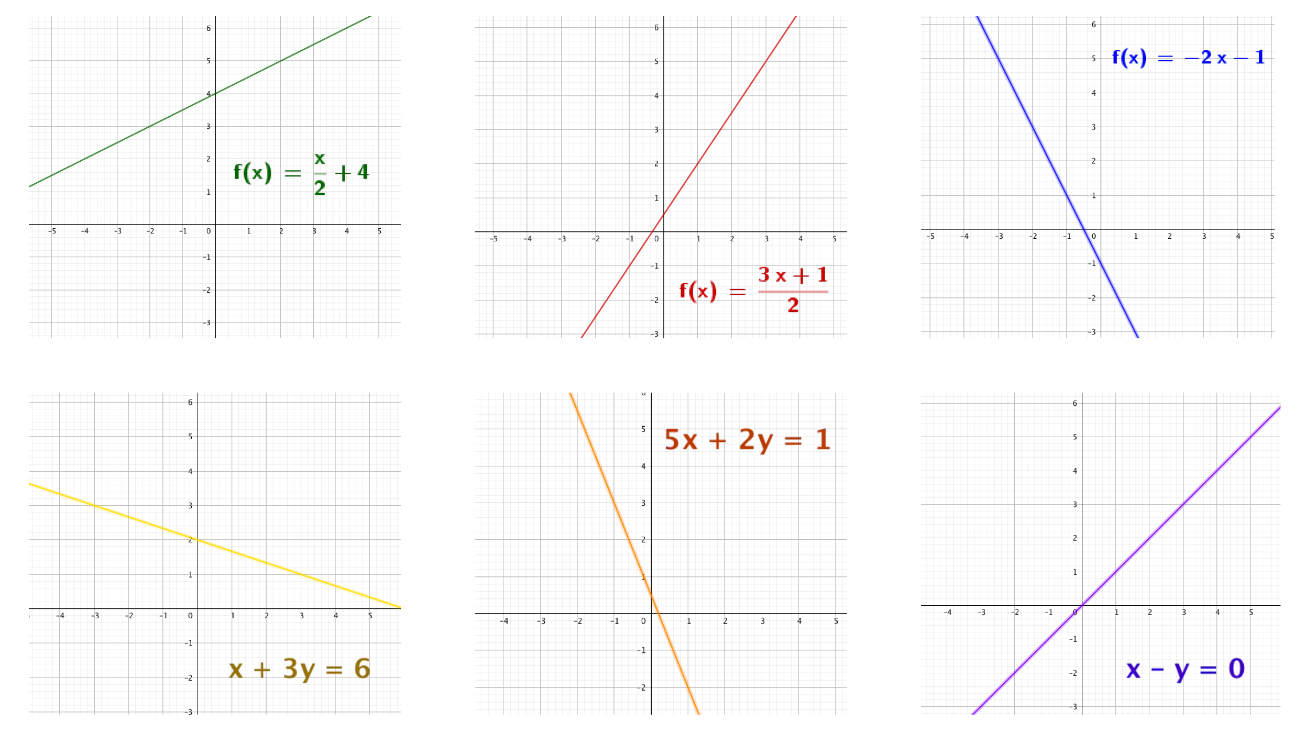
Una función lineal es una función de la forma o
¡Deberíais recordar qué es y qué es , vamos a verlo!
Ahora habiendo recordado esto, podemos pasar de la gráfica y de la tabla de valores a la expresión algebraica.
¡Vamos a ver cómo sacar de la gráfica la expresión algebraica!
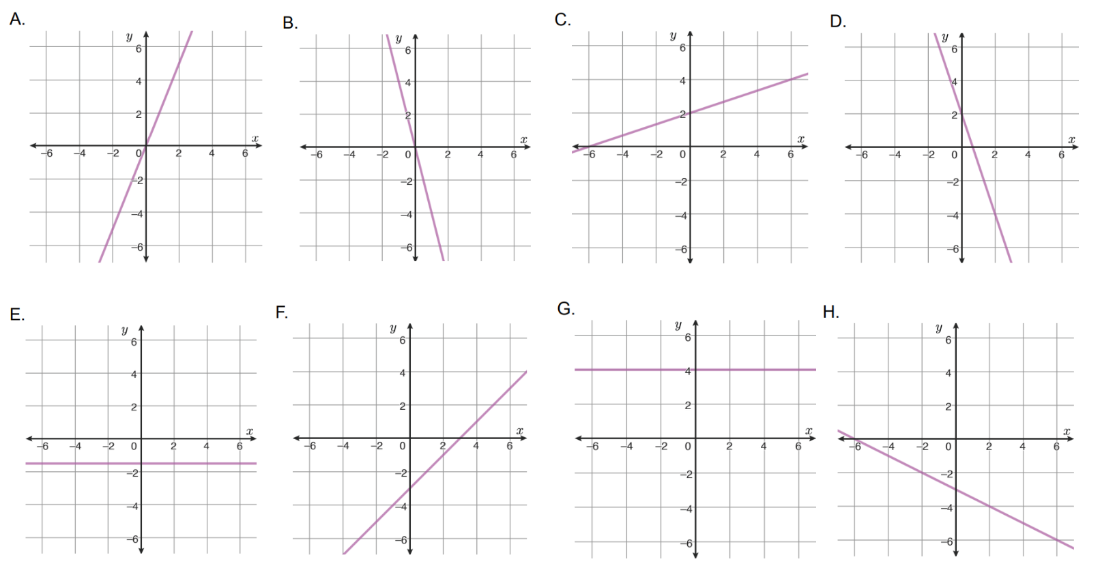
¿En las siguiente gráficas, la pendiente y la ordenada en el origen, son =, > o < que 0?
¡Para mañana!
Terminar la hoja y de la página 248 ej 8 y 9
3º Sesión - Seguimos con funciones lineales
Hoy vamos a hacer dos cosas más con funciones lineales y ya mañana pasamos a un tipo nuevo de funciones
¿Recordáis que vimos ayer?
- Todas las funciones lineales algebraicamente son de la forma f(x)=mx+n
- m representa la pendiente de la función
- n representa la ordenada en el origen
Y entonces... ¿Cómo podemos calcular el punto de corte con el eje x?
¡Intentadlo vosotros!
Ya hemos visto:
- Todas las funciones lineales algebraicamente son de la forma f(x)=mx+n
- m representa la pendiente de la función
- n representa la ordenada en el origen
- Cómo calcular los cortes con los ejes
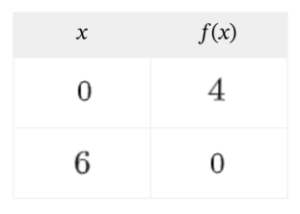
Si nos dan dos puntos de una función
¿Cómo podemos obtener la expresión algebraica de la función?
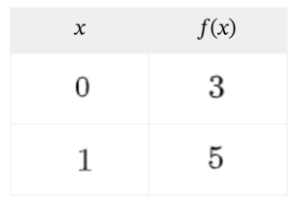
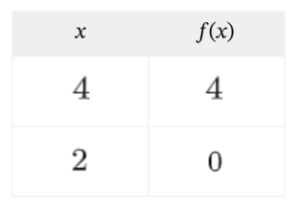

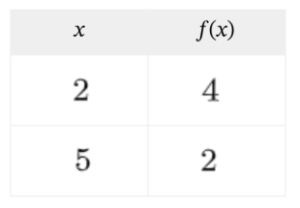
Para mañana: pág 258 ej 15 a y d, pág 259 ej 17 a y c
4º Sesión - Funciones cuadráticas
Estos días hemos estado viendo funciones lineales, que ya las conocíais de 2º de la ESO, pero ahora vamos a empezar algo nuevo, vamos a empezar con las funciones cuadráticas.
¿Cuál creeis que será la diferencia? ¿Qué os dice el nombre?
Efectivamente, las funciones cuadráticas están representadas por polinomios de grado 2
¿Qué forma suelen tener? Pensad en las ecuaciones de 2º grado
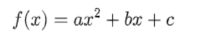
Ahora, os voy a pedir que hagáis una tabla de valores con las siguientes funciones que os voy a repartir y la idea es que intenteis representarlas uniendo los puntos.
Como ahora no sabemos qué forma van a tener estas funciones, vamos a dar más valores que en las lineales. Dad 5 valores y que 3 sean positivos y 2 negativos o viceversa.