II.1. Quadratur eines gleichseitigen Dreiecks
(nach Henry Ernest Dudney)
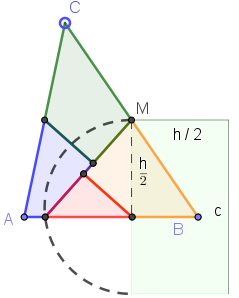
Im gleichseitigen Dreieck mit der Grundseite und der Höhe ist der Mittelpunkt der Seite und der Mittelpunkt von .
Das Dreieck hat den Flächeninhalt und ist flächengleich zum eingezeichneten Rechteck mit den Seiten und , dessen kurze Seite parallel zu liegt. Der Halbkreis über der Seite schneidet im Punkt . Nach dem Kathetensatz für das Dreieck gilt . ist also die Seitenlänge des flächengleichen Quadrats.
Für die Zerlegung wird noch ein Punkt benötigt, er erscheint bei Auswahl des Kontrollkästchens Konstruktionslinien. liegt auf und hat von den Abstand .
Von und werden die Lote auf gefällt, um das Dreieck in 4 Teile zu zerlegen.
Wählen Sie das Kontrollkästchen Teile bewegen, um das Dreieck zum Quadrat umzuwandeln (die Punkte werden dann ausgeblendet).
Der Abstand von zu ist nur geringfügig größer als , er beträgt ca. (Rechnung siehe Anhang). Dementsprechend erscheint beim Wechseln zwischen den Kontrollkästchen Dreieck & Rechteck und Konstruktionslinien Punkt ein wenig rechts von .
Anmerkung: Bei Dezimalbrüchen wird in diesem Buch in Anlehnung an die Schreibweise in GeoGebra-Applets der Punkt als Trennzeichen verwendet, und nicht das im Deutschen übliche Komma.
Innerhalb gewisser Grenzen ist diese Zerlegung auch für ungleichseitige Dreiecke möglich.