Esquema
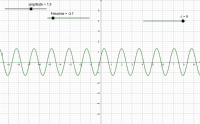
Grafik Sinus Interaktif
Grafik sinus adalah grafik dari fungsi:
y=sin(x)
y=sin(x)
yang berbentuk gelombang naik–turun secara berkala.
Grafik ini memiliki ciri-ciri:
Berulang setiap
360∘
360
∘
atau
2π
2π
Nilai paling tinggi = 1
Nilai paling rendah = –1
Melalui titik (0, 0)
2. Bentuk Umum Grafik Sinus
Untuk membuat grafik sinus interaktif, biasanya digunakan bentuk umum:
y=asin(bx+c)
y=asin(bx+c)
Di GeoGebra, nilai a, b, dan c dibuat slider, sehingga grafik bisa bergerak dan berubah bentuk.
3. Fungsi Setiap Parameter (a, b, c)
Ini bagian paling penting dari materi Grafik Sinus Interaktif.
⭐ 1. a → amplitudo (tinggi gelombang)
Mengubah nilai a membuat grafik menjadi tinggi atau pendek.
Jika a lebih besar → gelombang makin tinggi
Jika a kecil → gelombang makin pendek
Jika a negatif → grafik terbalik ke bawah
Contoh:
y=2sin(x)gelombang 2x lebih tinggi
y=2sin(x)gelombang 2x lebih tinggi
⭐ 2. b → frekuensi (kerapatan gelombang)
Mengubah b mengatur berapa banyak gelombang dalam satu periode.
b besar → gelombang makin rapat
b kecil → gelombang makin renggang
Periodenya menjadi
2πb
b
2π
Contoh:
y=sin(2x)gelombangnya 2x lebih rapat
y=sin(2x)gelombangnya 2x lebih rapat
⭐ 3. c → pergeseran (fase)
Mengubah c membuat grafik geser ke:
kanan (jika c negatif)
kiri (jika c positif)
Contoh:
y=sin(x+π)geser ke kiri sejauh π
y=sin(x+π)geser ke kiri sejauh π
4. Kenapa Disebut “Interaktif”?
Karena grafik berubah langsung ketika slider digeser.
Dengan slider di GeoGebra:
Geser a → tinggi grafik berubah
Geser b → gelombang jadi lebih rapat atau renggang
Geser c → grafik bergeser kiri/kanan
Siswa dapat melihat perubahan bentuk grafik secara visual tanpa menghitung manual.
5. Tujuan Pembelajaran Grafik Sinus Interaktif
Dengan media interaktif ini, siswa dapat:
Memahami bentuk grafik sinus secara visual
Melihat pengaruh masing-masing parameter
Menghubungkan konsep aljabar → grafik
Menjelaskan perubahan fungsi dengan mudah
Menggunakan teknologi (GeoGebra) untuk belajar matematika
6. Contoh Grafik Dasar Sebelum Interaktif
Jika slider belum digeser:
a = 1
b = 1
c = 0
Maka grafik adalah:
y=sin(x)
y=sin(x)
Titik penting:
puncak: (90°, 1)
lembah: (270°, –1)
periode: 360°