1.1 Prefacio
Personalmente considero que mucha más gente necesita álgebra lineal que cálculo. ¡Isaac Newton podría no estar de acuerdo! Sin embargo, él no está enseñando matemáticas en el siglo XXI. Ciertamente, las leyes de la Física se expresan bien mediante ecuaciones diferenciales. Newton requirió del cálculo, lo cual está bien. Pero el alcance de la ciencia, la ingeniería y la administración (así como de la vida) actualmente es mucho más grande, y el álgebra lineal se ha desplazado a un sitio central. Los datos se tomaron el mundo y hoy en día es necesario tener herramientas para analizarlos y sacar conclusiones de ellos, sorprendentemente el Algebra Lineal se ha posicionado de manera central en el área de Big Data, temas como la Descomposición Singular de Matrices (SVD) y El Análisis por Componentes Principales (PCA) son fundamentales para entender como varian los datos y cuál es la información más importante que ellos nos brindan. Bueno comencemos, tomemos dos vectores en el plano y que apuntan en direcciones distintas. El paso clave es tomar sus combinaciones lineales. Se multiplica cada vector por un número (escalar) para obtener por ejemplo los vectores 3 y 4, luego se suman estos para obtener una combinación particular 3 + 4. Este nuevo vector está en el mismo plano que y . Cuando se toman todas las combinaciones, se está llenando todo el plano. Si y se dibujan en esta página, sus combinaciones c + d llenan la página (y más allá), pero no salen de la página. Actividad:
- Mueva los deslizadores c y d para observar diferentes combinaciones lineales de los vectores y
- Use los botones para activar, desactivar y borrar el rastro del vector combinación (c + d)
Para encontrar combinaciones de estas columnas, la matriz se "multiplica" por un vector y así construimos la combinación lineal cv+dw:
Esta es una de las muchas maneras de multiplicar una matriz por un vector. Todas estas combinaciones para todos los valores de c y d no cubrirán todo el espacio tridimensional pero si generaran un plano en el espacio (¿Por qué?). Actividad:
- Mueva los deslizadores c y d para observar diferentes combinaciones lineales de los vectores y
- Use los botones para activar, desactivar y borrar el rastro del vector combinación (c + d)
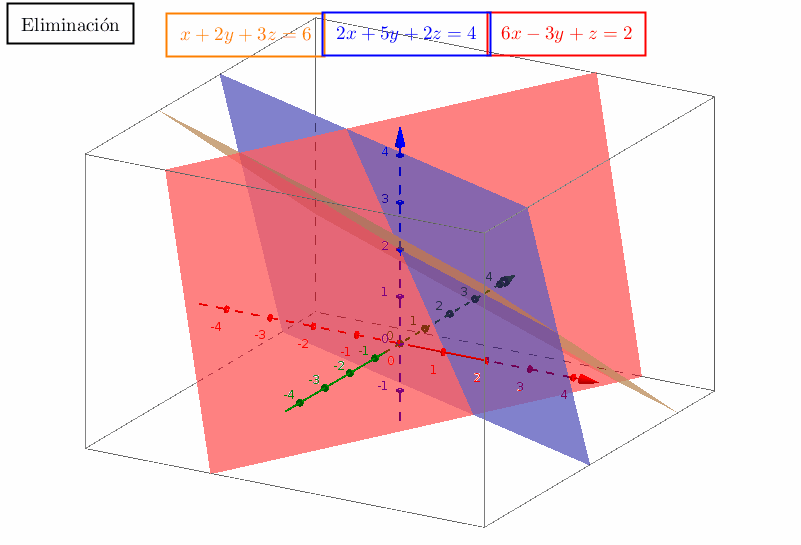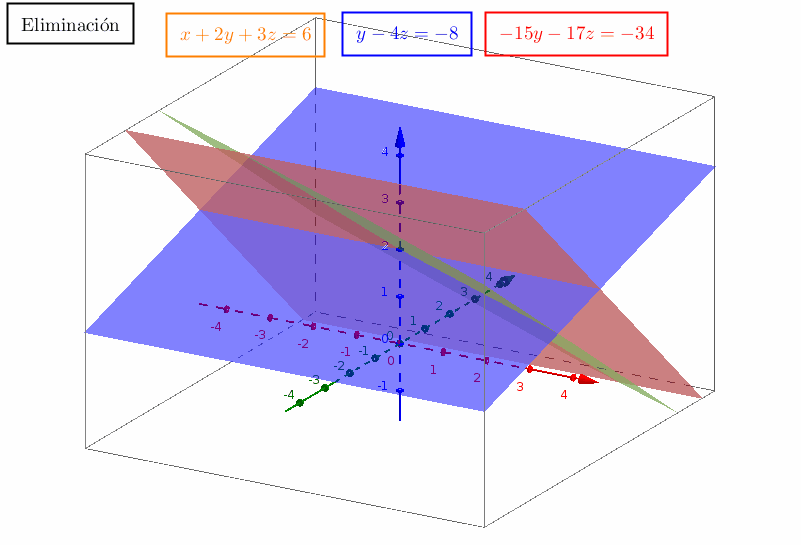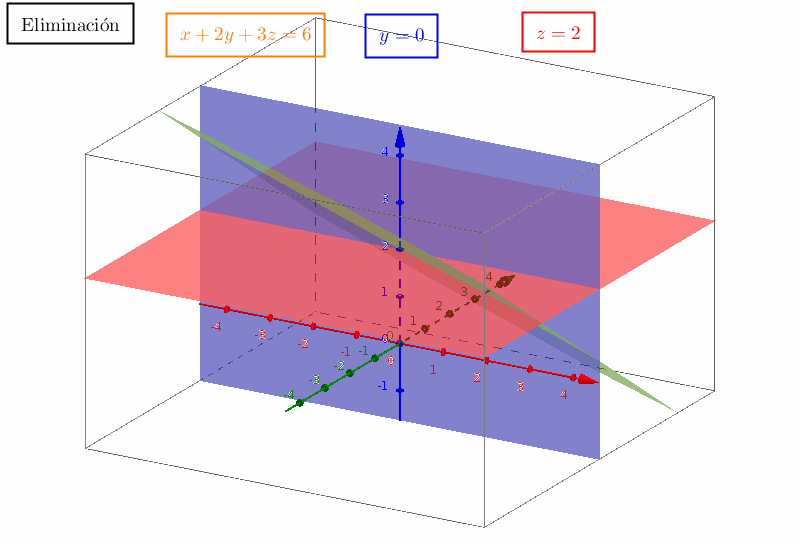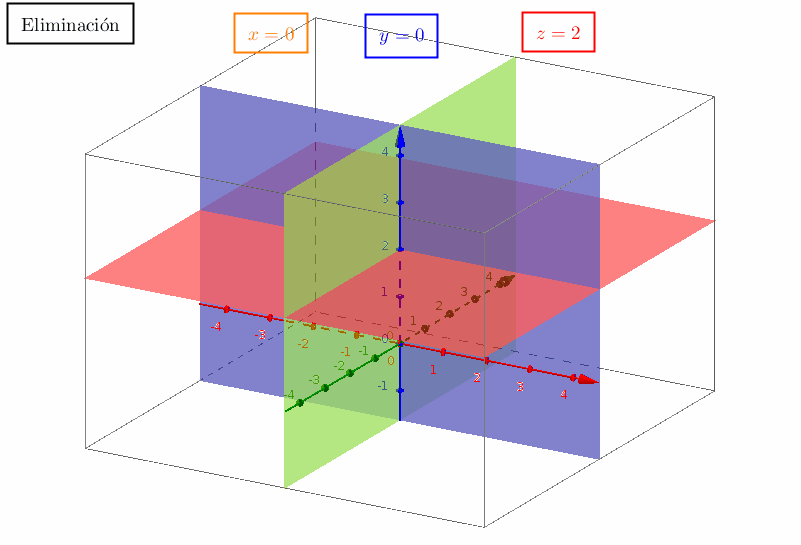
Estas combinaciones llenan un espacio vectorial, denominado espacio columna de la matriz. (Para estas dos columnas, dicho espacio es un plano.) Para averiguar si está en el plano, hay que resolver tres ecuaciones:Se deja que el lector las resuelva. El vector está en el plano de y . Si el 7 se cambia por cualquier otro número, entonces no estará en el plano ya que no es ninguna combinación de y por lo que las tres ecuaciones no tienen solución. La interacción de las columnas y las filas constituye el núcleo del álgebra lineal. No es totalmente fácil comprenderlo, aunque tampoco es tan difícil. A continuación se enumeran cuatro de los conceptos más importantes: 1. El espacio columna (todas las combinaciones de las columnas). 2. El espacio fila(todas las combinaciones de las filas). 3. El rango (el número de columnas independientes) (o filas). 4. Eliminación (la mejor manera de encontrar el rango de una matriz). Y aquí me detengo para permitirle recorrer el libro.