Galtonbrett
Das Galtonbrett geht zurück auf Sir Francis C. Galton (1822-1911).
In dieser Simulation werden Hindernisse - bei einer realen Umsetzung beispielsweise Nägel - in Form eines Dreiecks in 6 Reihen angeordnet. Die Wahrscheinlichkeit, dass eine Kugel bei einem Hindernis nach rechts fällt (mit der Wahrscheinlichkeit ) oder nach links fällt (mit der Wahrscheinlichkeit ), ist gleich groß: .
Die Verteilung der Kugeln in den sechs Behältern entspricht einer Binomialverteilung mit n = 6 und p = 0,5.
Berechnung der Wahrscheinlichkeiten
Die Zufallsvariable X gibt an, wie oft die Kugel den Weg nach rechts nimmt.
= 1·0,56 + 6·0,56 + 15·0,56 + 20·0,56 + 15·0,56 + 6·0,56 + 1·0,56
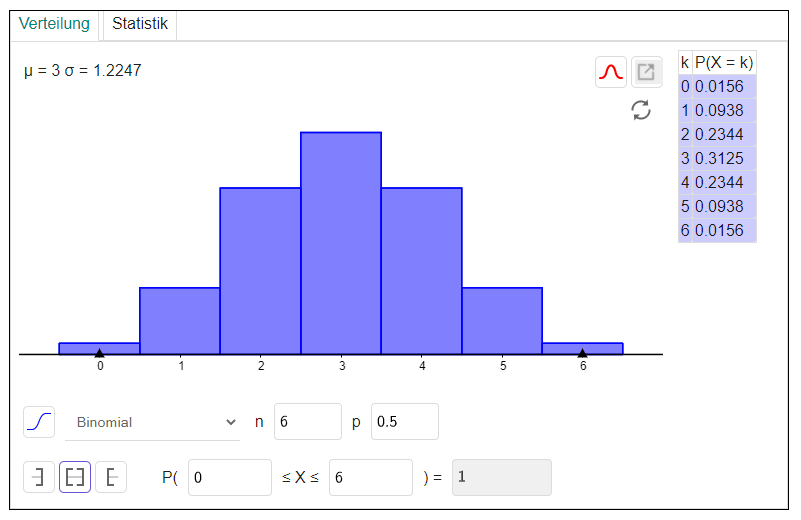
= 0,0156 + 0,0938 + 0,2344 + 0,3125 + 0,2344 + 0,0938 + 0,0156
Vergleich mit dem Wahrscheinlichkeitsrechner
Im Vergleich dazu die Wahrscheinlichkeitsfunktion für eine Binomialverteilung mit n = 6 und p = 0.50.