String and Pipe Modes
String Modes
When a vibrating string is supported at both ends and fixed in place as on string instruments the phase of the standing waves is fully determined. We know from the last section that an original wave traveling along the string must meet together with its doubly reflected counterpart with a phase difference . As we've seen before from this expression, when we substitute and consider that the doubly reflected wave travels twice the length of the string, or , we can see that . Cleaning this expression up leads to . These are all the allowable wavelengths on the string. It is easy to see that the longest wavelength is twice the length of the string, the second longest is equal to the length, etc.
Another useful fact is that the wave speed - as it true of light as well - does not depend on the wavelength, and since a standing wave really is made up of two traveling waves, the frequency is still governed by the equation . From this it should be clear that the longest wavelength produces the lowest frequency sound. The set of frequencies that will resonate on a tensioned string may be written
The lowest frequency that corresponds to N=1 is called the fundamental or the first harmonic. Note that all other frequencies will be integer multiples of this fundamental frequency. In other words . For waves on a string, in a few chapters we will derive the wave equation and show that the wave speed is dependent on the tension and on the linear density of the string, which is just the string's mass per unit length (kg/m) usually denoted In terms of those parameters,
Besides the fact that we have a phase relationship between any original wave and its doubly reflected counterpart, the actual waves also obviously can't have any amplitude at the points where they are tied to the instrument.
When there are points of zero amplitude along standing waves - like these points of attachment to the instrument - they are called nodes. Don't confuse this with normal modes which we'll define shortly.
The points that reach maximum amplitude rather than zero amplitude are called anti-nodes. When we consider both the allowable wavelengths from above and the fact that the nodes must be at the ends of the string, we can see what these waves must look like. Mathematically the members of the set of these allowable waves are called the normal modes of the system. Musically they are referred to as harmonics. Sometimes physicists and engineers will use both terms. The first ten are depicted below if you change the slider. Press play to see them animated and note the higher modes have proportionally higher frequencies of oscillation.
String Normal Modes
Pipe Modes
Recall that sound waves are longitudinal waves. That just means the disturbance travels parallel to the wave. If you look back at our chapter on waves you can see an animation of longitudinal sound waves. When they travel into or out of a pipe they reflect some of their amplitude even if the pipe ends are open! The extent to which they reflect depends on the impedance of the air. Impedance is a term used in many wave studies the most common of which is circuit impedance in early studies of electric circuits. Impedance both in that context and in this one relate to the ratio of a driving "force" to its effect. I put force in quotes since it doesn't have actual units of newtons, but is at least related to an actual force in newtons.
In circuits the driving "force" is a voltage, and the effect is the flow of electric current. The impedance . In the present context, the "force" is air pressure variation and the effect is the movement of air away from its equilibrium position. If a high pressure wave comes along and easily moves (shakes) the air through which it passes, the impedance is low. If, however, as in the case of air near the end a closed-ended pipe, the pressure wave comes along and can't move the air (since it's up against a wall), the impedance is high. Here's the vital point: Any time the impedance changes, we get reflections of waves. It turns out that a pressure wave has a harder time moving air inside a pipe than outside a pipe, and so the impedance inside a pipe is higher than outside a pipe.
The impedance relates to the wave speed in open-air conditions, and the relation is , where is the density of the air in this case. So you can see that high impedance means high speed. In this sense it's a lot like the inverse of refractive index. I mention refractive index because as with optics, we also here have the possibility of wave inversion upon reflection. The rule before was that waves bouncing off of a slower medium get inverted. The same rule applies now. In terms of impedances, bouncing off of a lower impedance inverts the wave.
I bring up the open-air connection between impedance and sound wave speed to draw connections to earlier knowledge in terms of wave inversions, but don't misunderstand me. Impedance is not like refractive index in all ways. Sound travels the same speed through air in pipes as it does in open-air, but the impedances are not the same. Reflection of waves depends really on mismatched impedances and not on the variation of the speed of sound in air.
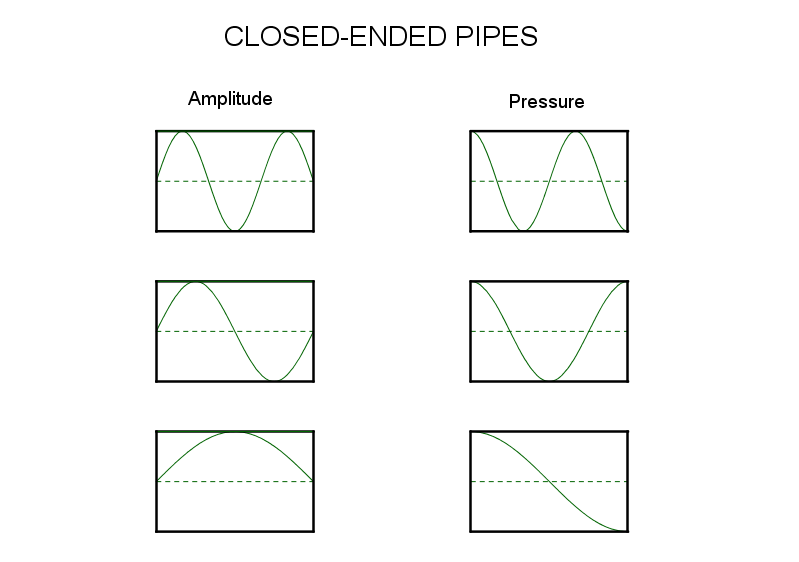
Closed Pipe Modes
How Open is Different
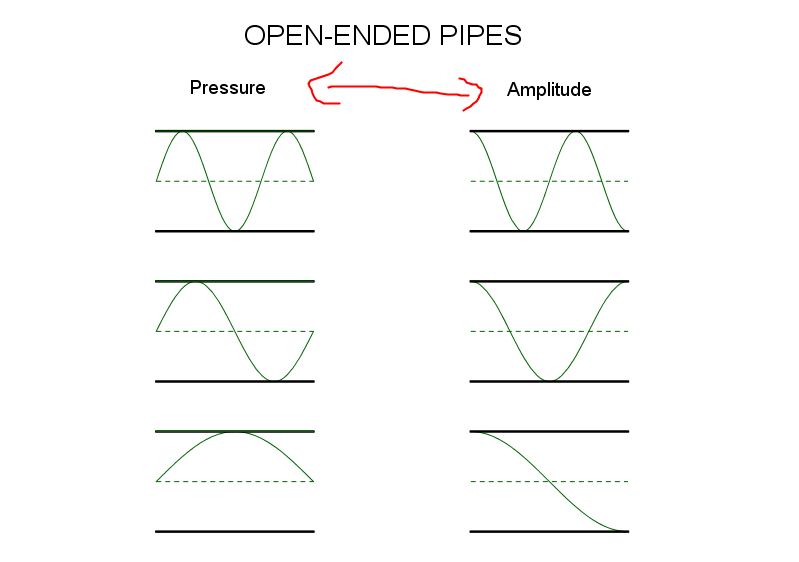
The only difference to the amplitudes and pressures for open-ended pipes is that the nodes have become anti-nodes and vice-versa. The overall phase difference between the original wave and its doubly reflected counterpart is still identical, or multiples of . What has changed is only the fact that the ends become maximum amplitude of air rather than minima. So the overall shape of the sine wave becomes a cosine wave for amplitude, for instance. The same frequencies are present in both since the wavelengths are identical.
Open Pipe Modes
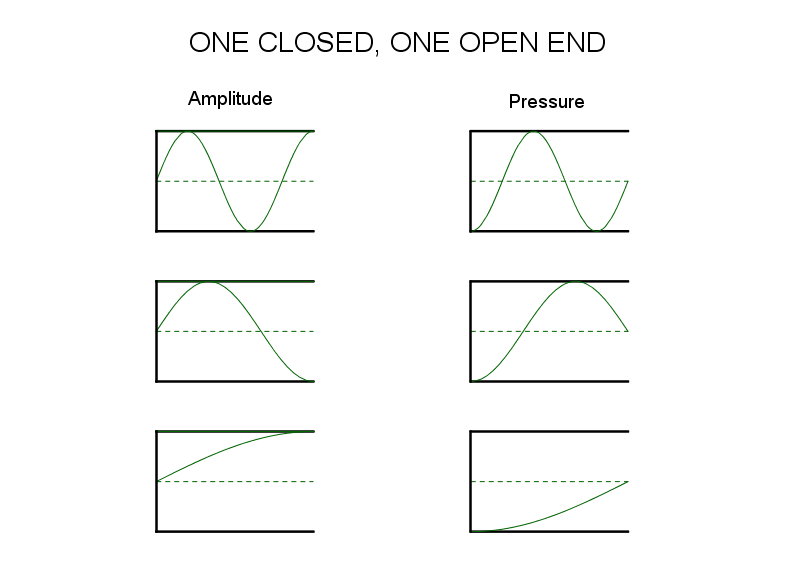
One Open End
When a pipe has only one end open, the situation is a bit different. We still should expect that an original wave must meet constructively with its doubly reflected self. The difference arises due to the reflection at the open end causing a wave inversion, or an additional phase change of . So we need If you look at the possible solutions for the path length induced term, the options are This is the entire reason for the difference for a pipe with only one open end. As usual, we can find the associated wavelengths by setting Cleaning this up, it's easy to see that the wavelengths must be given by this expression:
Look at this expression along with the picture of the first three modes shown in the diagram below and make sure you see how they go together. We will be measuring such modes in lab.
One Open End Modes
Self Test
If an open pipe, a closed pipe and a pipe with one end open all have the same length, which produces the lowest fundamental tone or pitch?
Normal Modes Versus Harmonics
While the terms normal modes and harmonics are generally interchangeable, there is one difference to note. If I mathematically label normal modes with N=1,2,3,4, then I would just speak of the N=1 or N=2 normal mode and it'd make sense.
In using the term harmonic, the harmonic number is not always equivalent to N. If you look at the frequencies for the string, the open pipe and the closed pipe, they all have frequencies that are integer multiples of the fundamental or first harmonic. In equation form, , and all Ns exist in those systems. In the pipe with only one end open, we only find frequencies corresponding to N=1, N=2, etc, even though we can write the expression of those frequencies using the notation.
When we speak of harmonics, we only ever mean one thing: The lowest tone is the first harmonic, and the second harmonic, if it exists, always has twice the frequency of the first harmonic. The third harmonic has triple that frequency, etc. So in the language of harmonics, a pipe with one open end only has odd numbered harmonics. In other words, the frequencies it resonates at are