Extremums Using Derivatives: The First Derivative Test

Auteur :Kaitlyn Bui

A derivative function has so many capabilities. Did you know you can find a function's local extremum using only its derivative? This is an essential skill in calculus, because there may be situations where no calculator is allowed, and/or you aren't given the original function or its graph.

The Plan:

Explore the relationship between local extrema and derivative functions
identify extremums of a function (ie. maximums, minimums) on an open interval by using the First Derivative Test
conclusion

Do you think you can do it? Let's explore!

Exploration
Look the graph

below. The local extrema are marked: points A, C are local minimums; point B is a local maximum.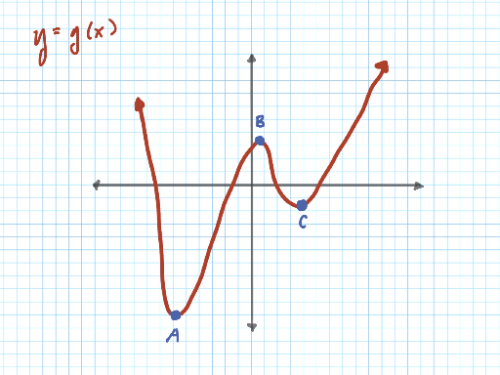

What do you notice about the graph surrounding the local extrema?

Vérifier ma réponse

The [color=#ff7700]orange[/color] indicates where [math]g[/math] is decreasing, and the [color=#1e84cc]turquoise[/color] indicates where [math]g[/math] is increasing. — The orange indicates where is decreasing, and the turquoise indicates where is increasing.

When there's a local minimum,

changes from decreasing to increasing. When there's a local maximum,

changes from increasing to decreasing. The image below shows how this property applies to a variety of functions.

The [color=#ff7700]orange[/color] indicates where the function is decreasing, the [color=#1e84cc]turquoise[/color] indicates where the function is increasing, and the [color=#ff00ff]pink[/color] indicates local extrema. — The orange indicates where the function is decreasing, the turquoise indicates where the function is increasing, and the pink indicates local extrema.

Now let's look at the graph of

. A, B, and C of

have the same x-value as the A, B, and C in

The [color=#ff7700]orange[/color] indicates where [math]g'[/math] is negative, and the [color=#1e84cc]turquoise[/color] indicates where [math]g'[/math] is positive. — The orange indicates where is negative, and the turquoise indicates where is positive.

Remember: where

is decreasing,

is negative. Where

is increasing,

is positive. This makes sense because a decreasing function has a negative slope, and vice versa.

According to the graph, points A, B, and C have a slope of 0. This means points A, B, and C are critical points. Critical points are points where the derivative of a function is equal to 0, or the value does not exist.

Look at the graph of again. What do you notice about the graph surrounding the critical points?

Vérifier ma réponse

Hmm... interesting. Now let's compare the graph of

with the graph of

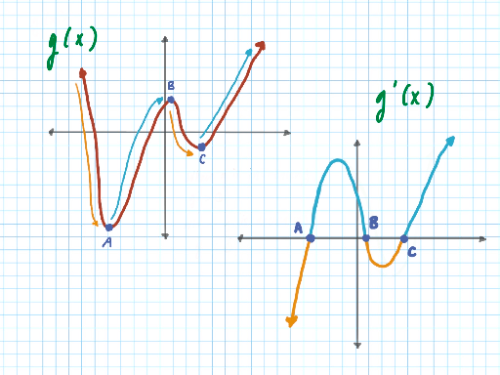
Note: the x-value of points A, B, and C remain the same in the derivative.

The derivative of local extremums A, B, C are also critical points. What can we conclude from this?

Vérifier ma réponse

Critical points can indicate where local extrema are. The graph surrounding critical points can also indicate what type of local extreme lies at that x-value.

We know A and C are local minimums. Look at A and C on : what happens to the graph at these points?

Vérifier ma réponse

We know B is a local maximum. Look at B on : what happens to the graph at this point?

Vérifier ma réponse

With this information, we can conclude two things: 1) there is a local minimum when a derivative function changes from negative to positive 2) there is a local maximum when a derivative function changes from positive to negative

Now let's apply what we learned to a problem.

The First Derivative Test

The function is continuous and differentiable for all x. Without a calculator, find the coordinates of the local minimum and maximum of if .

How do we go about this if we aren't given the graph of

? Well, lets use the First Derivative Test. First, we must find the derivative of

What is the derivative of ?

Vérifier ma réponse

Now that we have the derivative, let's find the critical points of

, or where

If , x = ?

Cochez votre réponse ici

A
x = 2
B
x = -2
C
x = -2, 2
D
x = 4

Vérifier ma réponse (3)

Great! Next Step: we need to make a sign chart.

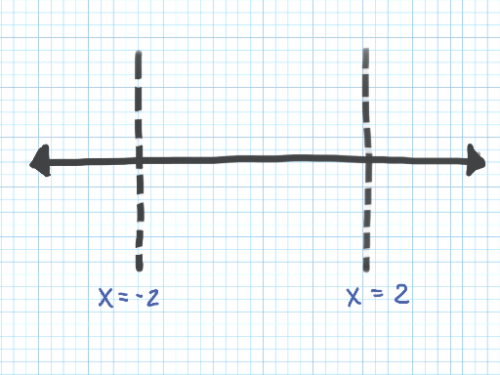
This is a sign chart. Sign charts are composed of a number line and asymptotes that are at the x-values of the critical points. In this problem, the asymptotes are at x=-2 and x=2.

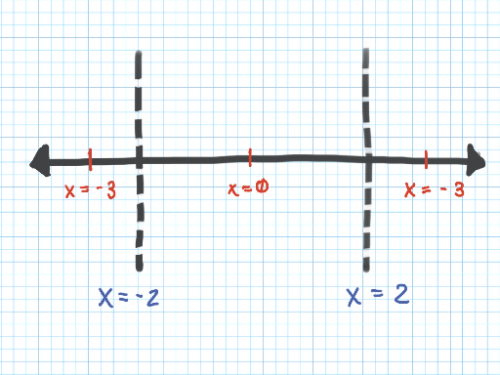
In the image above, notice we've created three sections: -∞ < x < -2, -2 < x < 2, and 2 < x <∞. Now we choose three x-values, one in each interval. Let's use x=-3, x=0, and x=3. Mark these values on your sign chart.

Let's go back to the derivative function

. Now we have to solve for f' when x=-3, x=0, and x=3. Are these values positive or negative?

, ,

Cochez votre réponse ici

A
+, +, +
B
+, -, +
C
+, +, -
D
-, +, -

Vérifier ma réponse (3)

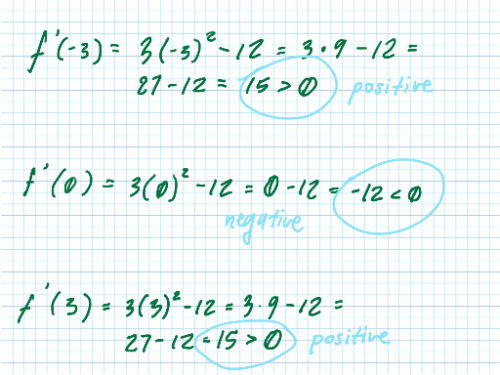
Great!

Now let's go back to our sign chart--we want to use our newfound information and apply it to the chart. We know

, and

. Let's put these symbols in their respective sections of the chart.

Looking at What We Learned Before 1) there is a local minimum when a derivative function changes from negative to positive 2) there is a local maximum when a derivative function changes from positive to negative Do you see why we marked the sections of the sign chart with either positive or negative symbols? We want to find where the function is decreasing or increasing, and these symbols tell us just that. Also, when a derivative function changes from positive to negative or vice versa, it occurs when the graph crosses the x-axis (or when the derivative = 0). This is why we use critical points to lead us to the extremums.

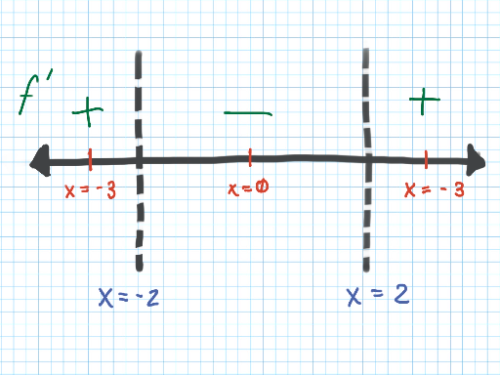
At what x-value does the local maximum occur? Justify your answer.

Vérifier ma réponse

At what x-value does the local minimum occur? Justify your answer.

Vérifier ma réponse

We're not done yet! The question asks for the coordinates, but we only have our x-values so far. We know

, so lets solve for

and

The local maximum occurs at (__,__). The local minimum occurs at (__, __).

Cochez votre réponse ici

A
(-2, 11) ; (2, -21)
B
(-2, 21) ; (2, -11)
C
(-2, -37) ; (2, 0)
D
(-2, 0) ; (2, -21)

Vérifier ma réponse (3)

Let's check our work! Use the GeoGebra applet below to find the local extrema of

. Use the extremum tool and click on the function.

Compare your answers to the actual answers. Are they the same?

Conclusion

What can we take away from this? We discovered by using the First Derivative Test, you can find the local extremum of a function on an open interval. Now you know a valuable skill for calculus that also applies to the real world! But what if the function is on a closed interval? Continue to the Candidates Test Activity to find out how.

Extremums Using Derivatives: The First Derivative Test

Great!

Nouvelles ressources

Découvrir des ressources

Découvrir des Thèmes