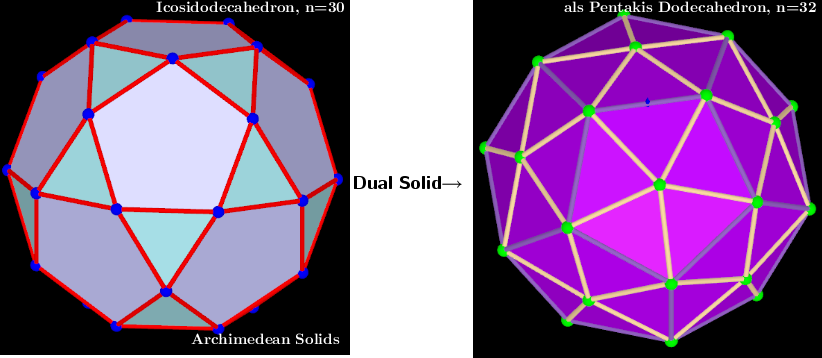
Icosidodecahedron, n=30. Polyhedra with extreme distribution of equivalent vertices. The coordinates of the polyhedron are taken from the applet : Polyhedra whose vertices are equivalent and have an extreme distribution on the same sphere.
The first applet sorts and finds the vertices, surface segments, faces, and volume of the polyhedron and its dual image.
The second applet colors the edges and faces of the polyhedron and its dual image.
All applets are in the Book : Polyhedra with extreme distribution of equivalent vertices :
Polyhedra whose vertices are equivalent and have an extreme distribution on the same sphere. * n=4: Tetrahedron ; n=6: Octahedron ; n=8: Cube , Square Antiprism ; n=12: Icosahedron , Cuboctahedron ,Truncated Tetrahedron ; n=20: Dodecahedron ; n=24: Biscribed Snub Cube , Truncated Cube , Biscribed Truncated Octahedron ; n=30: Icosidodecahedron ; n=48: Biscribed Truncated Cuboctahedron ; n=60: Biscribed Snub Dodecahedron , Rhombicosidodecahedron , Biscribed Truncated Icosahedron , Truncated Dodecahedron ; n=120: Biscribed Truncated Icosidodecahedron . This is a well-known polyhedron - Icosidodecahedron Vertices: 30 (30[4]) Faces: 32 (20 equilateral triangles + 12 regular pentagons) Edges: 60
This extreme distribution is obtained by me in the applet - "Three-parameter model transformations of the Icosahedron. Extreme distributions." -Special Case 5). t=0.5, q=1 and α=0. Icosidodecahedron, Vertices 30 and als Pentakis Dodecahedron, Vertices 32 Pentakis Dodecahedron -
Vertices: 32 (12[5] + 20[6]) Faces: 60 (isosceles triangles) Edges: 90 (60 short + 30 long)