The Geometry of Music

Overview

Music Basics - Defining Terms Origin of Music Theory - Pythagoras Relation to Group Theory Neo-Riemannian Tonnetz

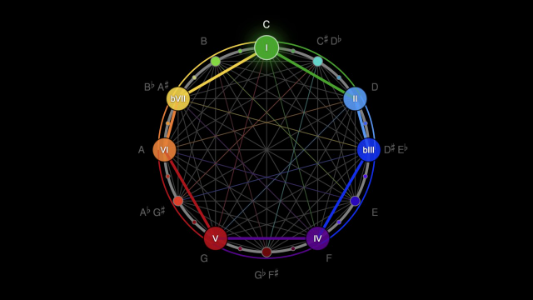
Getting some syntax out of the way

There are twelve distinct notes in an octave: C, C#, D, D#, E, F, F#, G, G#, A, A#, B (going up) B, Bb, A, Ab, G, Gb, F, E, Eb, D, Db, C (going down) For the purposes of this presentation, we'll be using sharps. Stepping through by one - half step (semitone) Stepping through by two - whole step (tone) Chord: Multiple notes played together Transposition: Playing a melody at a pitch higher or lower than the original pitch Inversion: Sending a note to its complement about a fixed center/reflection point (more later) Try it out here: String Demo

Origins of Music Theory

As with many concepts in mathematics, music theory finds much of its origin with Pythagoras. "All is number" - Pythagoras Pythagoras observed that different length strings produced different notes, and the notes produced correlated to their given string lengths, in particular: F = C/L, where F is frequency, C is some starting constant, and L is string length. So, for example, if we start with L = 1, we get F = C. If we cut the string length in half, we get F = 2C, correlating to a full octave jump in pitch.

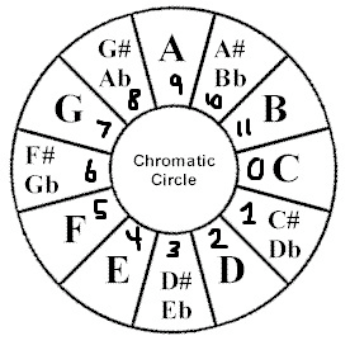
Chromatic circle

Now that we know a little more about pitch, let's talk about the chromatic circle above and its properties. If you're clever, you'll notice that since notes begin to repeat after the 12 notes above, we have a bijection between the set of pitch classes and

. Therefore, we can define a set of operations on the notes of a scale and do all our operations mod 12. For example, we can define transposition and inversion as follows:

(transposition by n semitones) ->

(inversion across n) ->

Element of the Chromatic Circle form a group under (+)

Proof: We'll call our set of pitch classes

, defined as such:

: [C C# D D# E F F# G G# A A# B] -> [0 1 2 3 4 5 6 7 8 9 10 11] Closure: Let a, b

. Then a, b correspond to elements of

, which is closed under addition, and thus a+b

. Identity: C acts as our identity in

. Let a

. Then a+C = a+0 = a. Inverses: As discussed, inversed exist for any axis/centerpoint. Let our centerpoint be n. Let a

. Then

= 2n - a. Since, again, every element corresponds to

, and a, n

, we know (2n-a)

. So every element has an inverse in

. Associativity: The addition operator is associative, giving us associativity. In addition,

comutes, making it an abelian group and therefore a cyclic group. In particular,

can be generated through repeated addition on the notes: C#(1), F(5), G(7), B(11) F0 = F F1 = A# F2 = D# F3 = G# F4 = C# F5 = F# F6 = B F7 = E F8 = A F9 = D F10 = G F11 = C F12 = F (starts over) This also means any subgroup of

will have order dividing 12. In fact, the subgroups directly correspond to the subgroups of

: {C}, {C, F#}, {C, E, G#}, {C, D#, F#, A}, {C, D, E, F#, G#, A#}

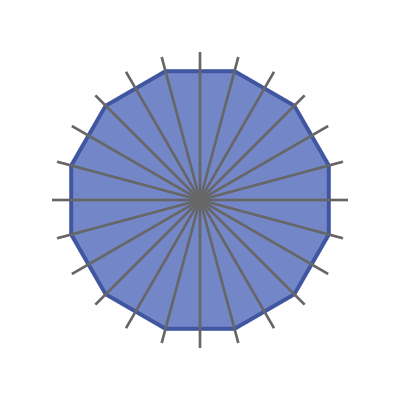
Even more interesting, the group of transpositions and inversions on

is isomorphic to the dihedral group

, the symmetries of a regular 12-gon. Transposition - rotation by 30

Inversion - reflection about a line of symmetry

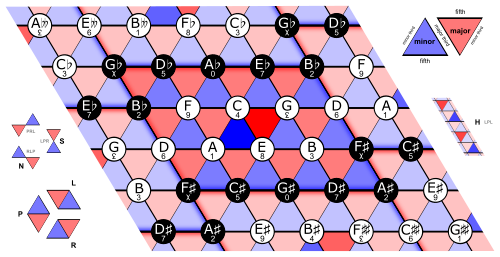
Neo-Riemannian Tonnetz

A way of visualizing chords using lattices. Every node is a pitch class, and every edge is either: perfect 5th, minor 3rd, or major 3rd. Chords are then represented by equilateral triangles, with each reflection along an edge representing: a switch between major and minor. Work with the following applet and tell me what patterns you can find among the lattice:

By Ewan Kummel Tonnetz

If we wrap around, considering the fact that pitch classes repeat after 12 elements, we can connect the tonnetz/lattice 3-dimensionally to get a torus.

Final Notes

This is just scratching the surface of what's out there in terms of music theory and mathematics. There's an entire field dedicated to it. Topics I haven't touched on include: Higher-prime tuning lattices, polyrhythms forming regular polygons, hyperbolic music maps, chord-stratified manifolds, quasicrystal scales, and about 100 others. Most of it is way over my head but if you're interested, this seems to be the leading publication in the field: