Arc Length and Sector Area
Check this out.
QUESTION 1
What happens when you double the central angle? 中心角を2倍にするとどうなるでしょうか?
QUESTION 2
Two sectors are created from the same circle. The central angle of the first sector is 30°, and the central angle of the second sector is 90°. Which of the following best describes the relationship between the central angle, arc length, and sector area in a circle? 円の中心角、円弧長、扇形面積の関係を最もよく説明しているのは次のうちどれですか?
QUESTION 3
Doubling the central angle doubles the arc length and the sector area. 中心角を 2 倍にすると、円弧の長さと扇形の面積も 2 倍になります。
QUESTION 4
The arc length and the area of sectors made from the same circle are not proportional to the measure of the central angles. 同じ円から作られる弧の長さと扇形の面積は、中心角の大きさに比例しません。
Let's Solve
Formula for solving the arc length and area of a sector.

PRACTICE 1
Given a sector with a radius r= 3m, and a 90°central angle, what is the arc length and sector area?
PRACTICE 2
Given a sector with a radius r= 3m, and a 120°central angle, what is the arc length and sector area?
Visualize
Watch this.
Central Angles Forming A Rectangle
Let's Solve
Formula in finding the area of the sector given the arc length and radius.
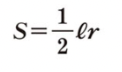
PRACTICE 3
Find the sector area. Given: r= 6 cm l= 4 π cm
PRACTICE 4
Find the sector area. Given: r= 9 cm l= 14 π cm
Let's Solve

PRACTICE 5
Find the central angle of a sector with a radius of 12 cm and an arc length of 10π cm.