Google ClassroomGoogle Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Funktionen: Definition

Autor:Maria Hänel
Wir wissen noch:

Bergwanderung

Du wanderst angefangen von der Höhe 50 auf einen Berg. Der Weg im Querschnitt des Berges ist in folgendem Koordinatensystem dargestellt. Nach 500 Metern Länge und 250 Metern Höhe kommt einen Bank.
Eine Zuordnung kann in einem Koordinatensystem dargestellt werden. Das Koordinatensystem enhält zwei Achsen, die [color=#6aa84f]Abszisse[/color] (x-Achse nach rechts) und die [color=#6aa84f]Ordinate[/color] (y-Achse nach oben).
Eine Zuordnung kann in einem Koordinatensystem dargestellt werden. Das Koordinatensystem enhält zwei Achsen, die Abszisse (x-Achse nach rechts) und die Ordinate (y-Achse nach oben).

Alternative Darstellung der Zuordnung

Eine andere Darstellung einer Zuordnung ist die Wertetabelle. Beispiel für die Bergwanderung:

x0??500375??
y??150300 ?? 150
Gib die fehlenden Zahlen an.

Revisa tu respuesta

Zuordnung: Wasserstrahl

Der Wasserstrahl in folgendem Applet hat die Zuordnung: Wassertropfenweite -> Wassertropfenhöhe Verwende das Punktetool (A) im Applet, um einen Punkt mit x-Wert und y-Wert zu erstellen.

Wertetabelle für Wasserstrahl

Verwende das Punktetool im Applet, um eine (ausreichend große) Wertetabelle für den Wasserstrahl (türkise Zuordnung) aufzustellen.

Arbeit mit Definitionen
Folgende Definitionen nennen dir in grün die mathematischen Vokabeln, die du wissen solltest und anwenden können solltest. Die Aufgaben danach fordern von dir eine "Interpretation der Defintion". Das bedeutet, dass du das Wort in grün in dem Beispiel mit dem Frosch-Wasserspeier finden sollst.

Definition

Der Definitionsbereich einer Zuordnung ist die Menge aller x-Werte. Eine Zuordnung, die jedem Wert von im Definitionsbereich genau einen Wert von zuordnet, nennt man Funktion.

Beispiel: Interpretation anhand der Bergwanderung

Beispiel: Interpretation anhand der Bergwanderung
Ich wandere angefangen x=0 auf einen Berg. Interpretation der Definition: Der Weg nach rechts wird auf der x-Achse angetragen. Die Definitionsmenge enthält also alle Distanzen vom Ursprung nach rechts. Der Weg nach oben wird auf der y-Achse angetragen. Der Berg hat keine Höhle, deswegen werden jedem x-Wert höchstens ein y-Wert zugeordnet. Der Berg hört nicht mittendrin auf, deswegen werden jedem x-Wert mindestens ein y-Wert zugeordnet Der Weg auf den Berg ist eine Funktion, weil sowohl mindestens als auch höchstens gilt (eben genau ein y-Wert zu jedem x-Wert zugeordnet wird).

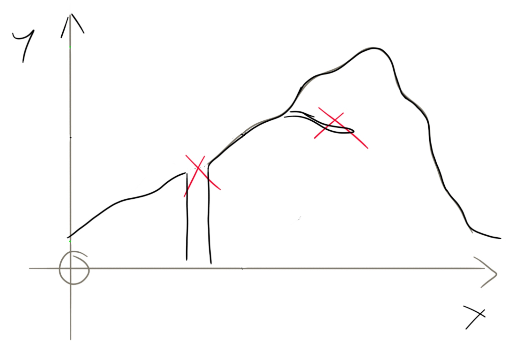
Interpretation anhand des Wasserstrahls

Interpretiere die Definition mittels des Beispiels des Frosch-Wasserspeiers. Das bedeutet: Stelle dir vor du sollst den Graphen eines solchen Wasserstrahls selbst zeichnen.

  • Welche Größe wird auf der x-Achse angetragen?
  • Welche auf der y-Achse?
  • Jedem x genau ein y: Gibt es x denen mehr als ein y zugeordnet wird oder x denen kein y zugeordnet wird?
  • Welche x-Werte würdest du auswählen, so dass der Wasserstrahl eine Funktion darstellt?

Revisa tu respuesta

Definition

Der y-Wert, der durch die Funktion zugeordnet wird, heißt Funktionswert an der Stelle .

Interpretation der Definition anhand des Wasserstrahls

Interpretiere die Definition mittels zweier Punkte der Wasserstrahl-Funktion des Frosch-Wasserspeiers. Das bedeutet: Wähle zwei beliebigen Punkt auf dem Graphen (am besten welche, die wir bereits kennen)

  • Nenne (x-Wert,y-Wert)
  • Nenne den Namen des Punktes
  • Gib an, welches der Funktionswert an der Stelle (des x-Wertes) ist.

Revisa tu respuesta

Definition

Als Funktionsgraph oder kurz Graph einer Funktion bezeichnet man die Menge aller geordneten Paare aus den x-Werten und den zugehörigen Funktionswerten . Wenn wir sagen "zeichne den Funktionsgraphen" meinen wir: Zeichne ein Koordinatensystem mit den x-Punkten und ihren zugehörigen Funktionswerten.

Definitionen schreiben und Graph zeichnen

Schreibe die Definitionen von Funktion, Funktionswert und Funktionsgraph in deinen eigenen Worten auf dein Merkblatt. Zeichne ein Koordinatensystem darunter, das den Graphen des Wasserstrahls (türkise Linie) enthält.

Nuevos recursos

Descubrir recursos

Descubre temas