ÇEMBER

トピック:円

GİRİŞ

Kazanım: M.6.3.3.1. Çember çizerek merkezini, yarıçapını ve çapını tanır. a) Pergel kullanmaya yönelik çalışmalara yer verilir. b)Çember ile daire arasındaki ilişki belirtilir.

Bir noktaya eşit uzaklıkta bulunan noktaların oluşturduğu düzlemsel şekle çember denir.

Günlük hayatta karşılaştığımız can simidi, bisiklet tekerleğindeki lastik ve simit birer çember modelidir.

KEŞFETME Sürgüyü hareket ettirerek çember çizimini yapınız.

AÇIKLAMA

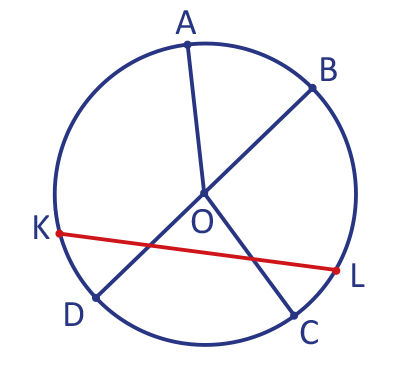
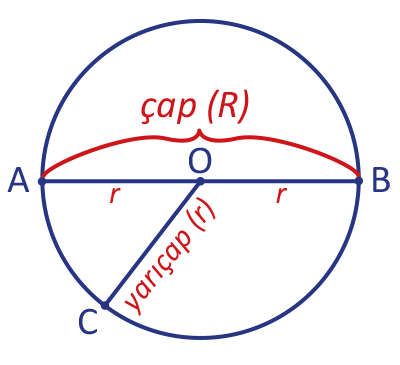
→ Düzlemde sabit bir noktaya eşit uzaklıktaki noktalar kümesine çember denir. → Çemberin tam ortasındaki sabit olan noktaya çemberin merkezi denir. Görseldeki çemberde “O” noktası çemberin merkezidir. → Çemberin merkezi ile çember üzerindeki bir noktayı birleştiren doğru parçalarının her birine yarıçap denir ve r ile gösterilir. Görseldeki çemberde [OA], [OC] ve [OB] yarıçaptır. → Çemberin üzerinde bulunan iki noktayı birleştiren ve çemberin merkezinden geçen doğru parçasına çap denir ve R ile gösterilir. Görseldeki çemberde [AB] çaptır.

Aşağıdaki O merkezli çember için merkez, yarıçap ve çapı belirleyelim ve yazalım.

答えを確認

DERİNLEŞTİRME

ÇEMBERİN DÜZLEMDE AYIRDIĞI BÖLGELER Bir çember çizildiği düzlemi üç bölgeye ayırır: → Çemberin iç bölgesi → Çemberin dış bölgesi → Çemberin kendisi

Sürgüyü hareket ettirerek çemberin merkezi, çapı ve yarıçapının değişimini gözlemleyiniz.

Daire ile çember arasındaki fark nedir?

Çember ile Daire Arasındaki İlişki

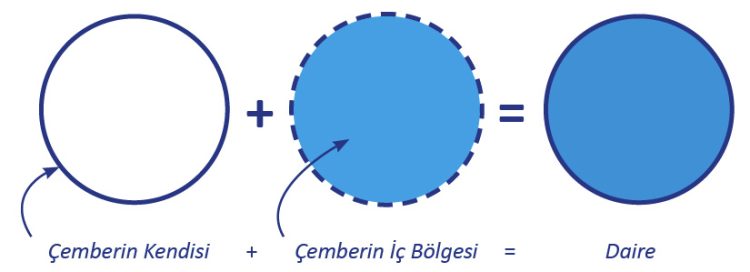
Bir çemberin kendisi ve iç bölgesinden oluşan geometrik şekle daire denir

Çemberin içi boş iken dairenin ise içi doludur. Yani daire çember ile çemberin iç bölgesinin birleşiminden oluşmaktadır. Bunun haricindeki diğer bütün özellikleri ise aynıdır. ÖRNEK: Çember ve daireye çevremizden örnekler verelim. Çevremizdeki çember modelleri: Yüzük, can simidi, basketbol potası, su bardağının ağız kısmı, simit, hula hop, bilezik, bisiklet tekeri, bant ve benzerleri. Çevremizdeki daire modelleri: Madeni paralar, çeyrek altın, gram altın, pizza, madalya, konserve kapağı, su bardağının dip kısmı ve benzerleri.

ÇEMBER ÇİZİMİ

Madeni para, tabak, içecek kutusu gibi eşyaları kağıt üzerine koyup etrafından kalemle çizgi çizerek çember elde edebiliriz. Ancak belirli ölçülere sahip yani istediğimiz büyüklükte bir çember çizebilmemiz için pergel ve cetvele ihtiyaç duyarız. Şimdi pergel ile çember çizmeyi adım adım görelim. 1. Adım: Pergelin bir kolunu cetvelde 0’a, diğer kolunu ise istediğimiz sayıya getiririz. Kollar arasındaki bu uzunluk, çizeceğimiz çemberin yarıçap uzunluğu olur. 2. Adım: Pergelin iğnesini kağıtta istediğimiz bir yere batırırız. Batırdığımız bu nokta çemberimizin merkezi olur. 3. Adım: Pergeli iğnesinin etrafında, kalemli kolu defteri çizecek şekilde tam tur döndürürüz. Çizdiğimiz bu çizgi çemberimiz olur.