Understanding Graphs of Trig Functions
Make sure ONLY the Sin(x) box is checked!
Adjust the amplitude slider in the applet so that it's at 3. What is the distance from the maximum to the minimum on the function g(x). How does that relate to an amplitude of 3?
If a Sine function is transformed so it has an amplitude of 6, what will the equation look like?
Adjust the amplitude back to 1 then adjust the frequency slider so that it's at 2.
What does changing the frequency do to the sine function?
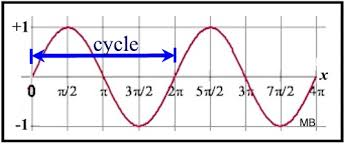
When you adjust the frequency to 2 on the applet, how many full cycles on the red g(x) function can be seen between 0 and 2?
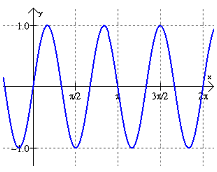
Adjust the frequency slider back to 1. Change the "vertical" slider so that it's at 2
What does changing the vertical slider do to the function?
If you wanted to take a sine function and slide it down 4 units, what would be the equation of the new function?
You can do MORE than one of these things at once!
If you want to take a function, change its amplitude so that it's 2, adjust the frequency so that it's 4 and slide the function up 2 boxes, what would its equation look like? (Hint: You can use the applet to help!)
Lets try some with COSINE!
Make sure the Cos(x) box is checked!
Adjust the sliders for amplitude, frequency and vertical shift. How does these changes compare to the changes in the sine function?
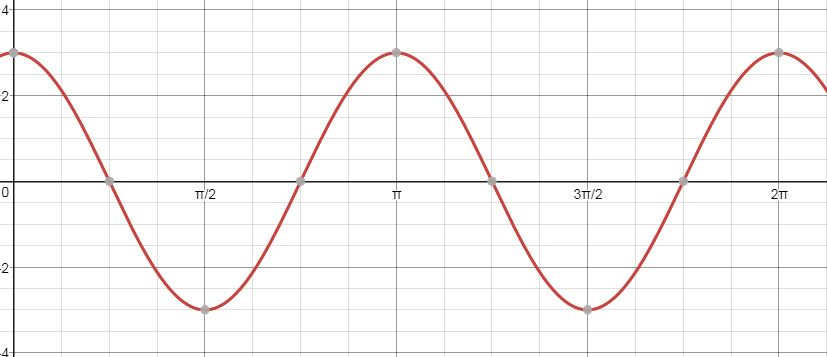
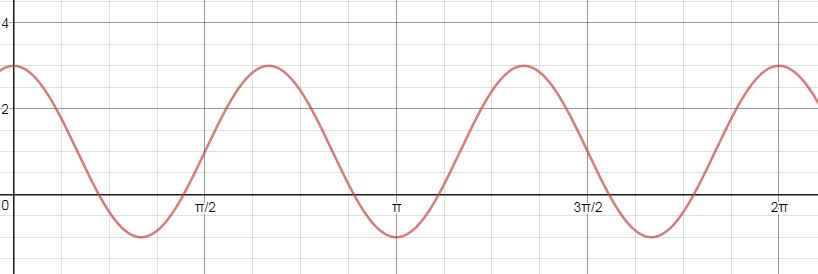
If you want to take a cosine function, change it so that the distance between the maximum and minimum is 8, so that it has 4 cycles between 0 and 2, and slide the function down 2 boxes, what would its equation look like? (Hint: You can use the applet to help!)