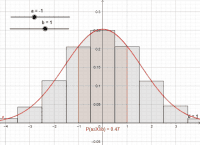
Stetige Zufallsgrößen - Normalverteilung

"Die Wahrscheinlichkeiten ganzzahliger Zufallsgrößen kann man mit Pfad- und Summenregel berechnen. Bei reellwertigen Zufallsgrößen geht das nicht mehr. Man greift auf Integrale zurück und erweitert damit den Einsatzbereich der Integralrechnung erheblich. Im Mittelpunkt steht die Gauß´sche Glockenfunktion, die als Normalverteilung eine Brücke schlägt zwischen Analysis und Wahrscheinlichkeitsrechnung. Der zentrale Grenzwertsatz erklärt, warum die Normalverteilung in Wirklichkeit so oft vorkommt."