Making the Moves
Making the Moves Summary
1.4 Making the MovesUNIT 1 • LESSON 4 MAKING THE MOVESSetting the StageWHAT YOU WILL LEARNIn this lesson, I will draw and describe translations, rotations, and reflections.I can...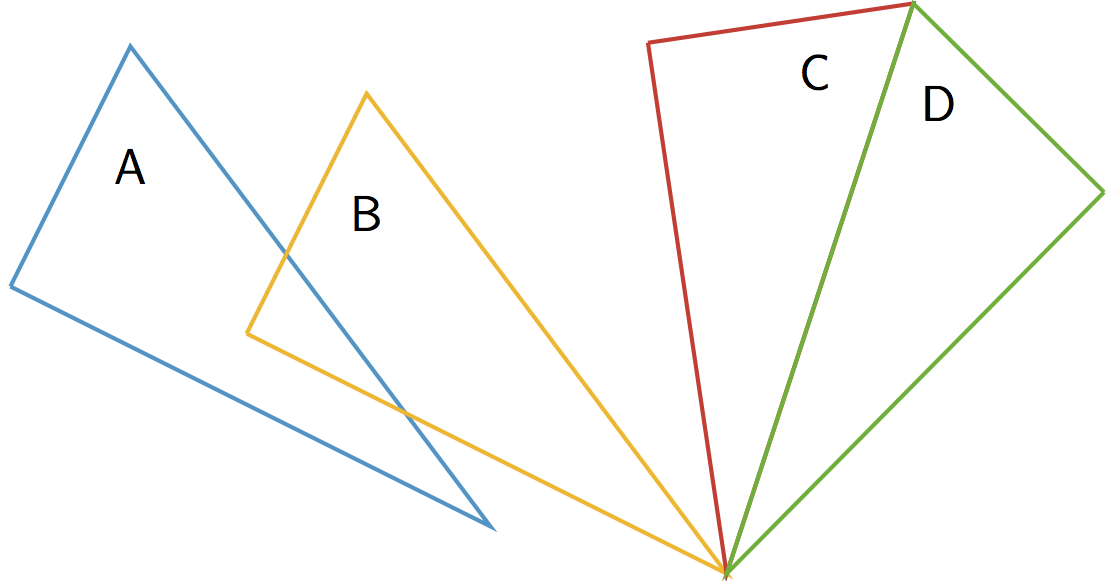 FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.4.1: Reflection Quick ImageHere is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.Geogebra Applet (Links to an external site.)Links to an external site.4.2: Make That MoveYour partner will describe the image of this triangle after a certain transformation. Sketch it here.Geogebra Applet (Links to an external site.)Links to an external site.4.3: A to B to CHere are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)
FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.4.1: Reflection Quick ImageHere is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.Geogebra Applet (Links to an external site.)Links to an external site.4.2: Make That MoveYour partner will describe the image of this triangle after a certain transformation. Sketch it here.Geogebra Applet (Links to an external site.)Links to an external site.4.3: A to B to CHere are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)
 All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
- Given a figure and a translation, rotation, or reflection, draw the image of the figure under the transformation.
- Given two figures, identify and describe a sequence of two transformations that takes one figure to another.
- Demonstrating that I can use the terms translation, rotation, and reflection to precisely describe transformations.
 FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.4.1: Reflection Quick ImageHere is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.Geogebra Applet (Links to an external site.)Links to an external site.4.2: Make That MoveYour partner will describe the image of this triangle after a certain transformation. Sketch it here.Geogebra Applet (Links to an external site.)Links to an external site.4.3: A to B to CHere are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)
FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.4.1: Reflection Quick ImageHere is an incomplete image. Your teacher will flash the completed image twice. Your job is to complete the image on your copy.Geogebra Applet (Links to an external site.)Links to an external site.4.2: Make That MoveYour partner will describe the image of this triangle after a certain transformation. Sketch it here.Geogebra Applet (Links to an external site.)Links to an external site.4.3: A to B to CHere are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)- Name a transformation that takes Figure A to Figure B. Name a transformation that takes Figure B to Figure C.
- What is one sequence of transformations that takes Figure A to Figure C? Explain how you know.
- Select the Vector tool.
- Click on the original point and then the new point; you should see a vector.
- Select the Translate by Vector tool.
- Click on the figure to translate, and then click on the vector.
- Select the Rotate around Point tool.
- Click on the figure to rotate, and then click on the center point.
- A dialog box will open; type the angle by which to rotate and select the direction of rotation.
- Select the Reflect about Line tool.
- Click on the figure to reflect, and then click on the line of reflection.
- No rotations?
- No reflections?
- No translations?
- A translation can be described by two points. If a translation moves point A to point A′, it moves the entire figure the same distance and direction as the distance and direction from A to A′. The distance and direction of a translation can be shown by an arrow.For example, here is a translation of quadrilateral ABCD that moves A to A′.

- A rotation can be described by an angle and a center. The direction of the angle can be clockwise or counterclockwise.For example, hexagon ABCDEF is rotated 90∘counterclockwise using center P.

- A rotation can be described by an angle and a center. The direction of the angle can be clockwise or counterclockwise.For example, hexagon ABCDEF is rotated 90∘counterclockwise using center P.
- A reflection can be described by a line of reflection (the “mirror”). Each point is reflected directly across the line so that it is just as far from the mirror line, but is on the opposite side.For example, pentagon ABCDE is reflected across line m.

 All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.