Altri tipi di parabola
Consideriamo l'espressione . Notiamo che ha la stessa forma dell'equazione di una parabola, dove però sono state invertite le e le .
Di conseguenza facendone il disegno potremo dedurre:
- che avrà l'asse di simmetria parallelo all'asse delle , invece che a quello delle ;
- poiché il suo coefficiente , cioè il coefficiente di - attenzione! - , è positivo, avrà la concavità rivolta verso l'"alto" delle , cioè verso destra (le crescono verso destra);
- la sua - attenzione, le lettere sono invertite! - avrà valore , e sostituendola si trova
QUESTA NON È UNA FUNZIONE!
Dal punto di vista geometrico la situazione è chiara.
Cerchiamo invece di approfondire il significato di una curva disposta in questo modo quando la interpretiamo come rappresentazione di una relazione tra due grandezze delle e delle .
L'utilizzo che si fa convenzionalmente del piano cartesiano quando lo si usa per rappresentare delle relazioni o delle funzioni prevede di porre sull'asse orizzontale la variabile indipendente, cioè l'input da cui si parte per ottenere il risultato, e che tale risultato venga collocato sull'asse . Una funzione infatti ha il formato , ed in particolare , dove è l'espressione che ci permette di calcolare la .
Esplicitiamo allora lettera , per ottenere un formato che ci permetta più chiaramente di calcolarne il valore a partire da una certa .
Invertiamo la sua equazione rispetto ad :
Questo è coerente con la figura ottenuta sopra, infatti
- il dominio dell'equazione è dato dalle C.E. cioè , infatti si vede anche in figura che la nostra parabola "esiste", cioè dà risultati, solo da in poi;
- NON è una funzione di , infatti dato un valore di otteniamo due valori di , ad esempio con abbiamo e , come puoi vedere dalla figura.
La parabola prende sia i risultati superiori che quelli inferiori; quando estraiamo la radice possiamo scegliere di considerarne uno solo dei due.
Nell'esempio che segue facciamo il percorso inverso da quello visto ora.
ESEMPIO 1
Come è fatta la curva ?
Vediamo che
- il suo dominio è dato dalle C.E.
- Notiamo inoltre che davanti alla radice c'è un segno meno, quindi il risultato si ottiene togliendo a una quantità positiva (la radice).
Ora per capire meglio la forma della curva eleviamo al quadrato per eliminare la radice, non prima di averla isolata per evitare di dover fare un quadrato di binomio con una radice dentro:
Svolgendo i calcoli (da notare che il davanti alla radice sparisce, e quindi perdiamo l'informazione che la scendeva rispetto a , ecco perchè ne abbiamo tenuto traccia prima)
Abbiamo esplicitato rispetto alle perché era di primo grado e quindi più semplice. Vediamo che si tratta di una parabola orizzontale "triste", cioè verso destra, con vertice , otteniamo sostituendo .
Il vertice è quindi . Aggiungiamo al piano una parabola con queste caratteristiche.
Da notare che la parabola, tratteggiata, ha perso l'informazione che ci diceva che la curva originale aveva "scelto" le sotto il 3. Quindi la parabola non è una funzione - per ogni nel proprio dominio fornisce due risultati - mentre l'equazione con la radice sì, perchè tra questi due risultati sceglie di prendere solo quello minore che scende rispetto a .
Abbiamo perso l'univocità del risultato quando abbiamo elevato al quadrato, che in generale NON mantiene un'equazione equivalente alla precedente ma rischia di aggiungere soluzioni non presenti prima. Infatti se prendiamo l'equazione
essa ha una sola soluzione, ma elevando al quadrato abbiamo , che come sappiamo ha due soluzioni - ma anche , che non era presente originariamente.
È comunque utile passare attraverso la parabola, che è una curva semplice e che conosciamo, per capire meglio come è fatta la funzione - basta ricordarsi di togliere le parti che non fanno parte della curva originale.
LE PARABOLE CON ASSE PARALLELO ALLE X COME FUNZIONI INVERSE
Abbiamo detto che le parabole con asse di simmetria orizzontale di fatto hanno invertito le con le .
Sul piano cartesiano, quando si parla di funzioni, le hanno un significato ben preciso: sono la variabile indipendente, l'input che si sceglie per calcolare il risultato. Allo stesso modo l'asse delle è quello lungo il quale si riporta questo risultato.
Invertire le due variabili, quindi, significa scambiare di ruolo la grandezza di partenza con il risultato finale. Si ottiene quella che è chiamata funzione inversa dell'originale.
ESEMPIO 2: La funzione mi permette di calcolare la temperatura in base all'età (che possiamo pensare misurata in miliardi di anni); in questo caso rappresentandola sul piano cartesiano metterò il tempo sulle e la temperatura che la stella ha in quell'istante, e che ottengo come risultato della funzione, sulle .
Dal grafico si può vedere che la stella 3 miliardi di anni fa era alla temperatura di zero gradi, ha raggiunto la massima temperatura oggi, quando inizierà lentamente a diventare senza più fredda fino a tornare a zero fra tre 3 miliardi di anni. Ovviamente si tratta di un'ipotesi priva di reale valore scientifico, serve solo come esempio.
Se calcolo la funzione inversa ricavando , questa mi permetterà di calcolare, partendo da una certa temperatura , il corrispondente età in cui la stella ha quella data temperatura.
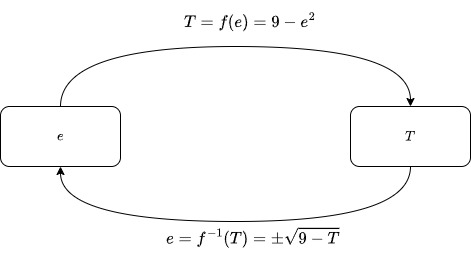
Per questa funzione l'età è diventato il risultato e quindi finirà sulle e l'altezza è ora il dato di partenza e sarà sulle , di conseguenza il suo grafico sarà identico a prima, ma con gli assi scambiati.
Abbiamo invertito parzialmente la funzione: la relazione è rimasta la stessa, l'abbiamo solo "impaginata" in modo diverso mettendo le temperature sull'asse delle , dato che sono il nuovo input, e le età sull'asse delle , poichè ora sono il risultato. Infatti possiamo leggere il grafico cercando una temperatura sulle e trovando le corrispondenti età lungo le . Ad esempio la rig tratteggiata verde risponde alla domanda "Quand'è che la stella ha temperatura 8 milioni di gradi?" dando la risposta "sia tra un miliardo di anni () che un miliardo di anni fa (). Da questo esempio si vede che l'inversa di non è una funzione, dato che non garantisce l'unicità del risultato.
Abbiamo invertito solo "graficamente" la funzione. Per farlo anche dal punto di vista matematico dobbiamo ricavare , in modo da ottenere l'espressione che ci permette di calcolarla a partire da un certo valore di . Con alcuni semplici passaggi algebrici ottengo
Il calcolo svolto, ed in particolare il doppio segno che abbiamo dovuto aggiungere estraendo la radice, mette in evidenza che la nuova relazione ottenuta non è una funzione in quanto ha due risultati uguali ed opposti. È come se la relazione fosse l'unione di due funzioni.
[size=85]Una parabola con asse di simmetria parallelo all'asse delle non è una funzione; può essere vista come unione di due funzione, una che fornisce i risultato del "ramo superiore" ed una che genera quelli del "ramo inferiore".
Puoi trovare più dettagli sulle funzioni inverse a questo indirizzo: https://www.geogebra.org/m/ahCuGvXP#material/ujautySS