A Counterexample
Let us look at the set of ordered pairs that satisfies the equation . Here is a graph of the ordered pairs that satisfy this equation.
Here is a partial list of the ordered pairs that satisfy this equation. (There are infinitely many ordered pairs, so it would be unreasonable to write them all out explicitly.)
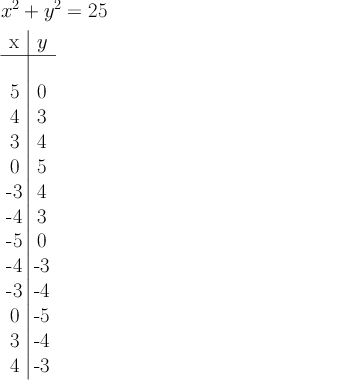
Notice that the ordered pairs (4,3) and (4,-3) both satisfy the equation. So here we have identified an input value (4) that has two possible output values (3 or -3).
The definition of a function states that it is a set of ordered pairs in which each input value is identified with exactly one output value. Therefore we can conclude that the set of ordered pairs satisfying the equation is not a function.
Sometimes mathematicians will say that a function has to pass the "vertical line test". By this they mean that if you have a function whose ordered pairs are graphed, each vertical line in the graphing plane can intersect with the graph at most one time. We can see that the vertical line intersects the graph of in two places: (4,3) and (4,-3). Thus by the vertical line test, the set of ordered pairs that satisfy the equation is not a function.
In fact you could enter any equation of the form where b is a value between -5 and 5, and see that the corresponding vertical line intersects the circle in two points. So there are many vertical lines showing that is not the equation of a function. Because of this we say that the graph of does not pass the vertical line test.
So is not the equation of a function. Or, to state it using the definition of a function, is not a function.