Unidades de medida de Volume & Cilindros
Assista!
de Pi ao cilindro
O Valor de Pi:
Pi (π) é uma constante matemática que representa a relação entre a circunferência de um círculo e seu diâmetro. É aproximadamente igual a , mas sua representação decimal é infinita e não periódica, o que significa que seus dígitos não se repetem em um padrão específico.
Fórmula da Circunferência:
A circunferência de um círculo pode ser calculada usando a fórmula:
onde C é a circunferência e r é o raio do círculo. Aqui, representa o comprimento da circunferência para um dado raio.
Área do Círculo:
A área A de um círculo é calculada por:
onde r é o raio do círculo. Essa fórmula expressa a quantidade de espaço dentro dos limites do círculo.
Volume de um Cilindro:
O volume V de um cilindro, que é formado por um círculo de base e uma altura h, pode ser determinado por:
Nesta equação, r é o raio da base do cilindro e h é sua altura. Essa fórmula é essencial para calcular o espaço tridimensional que o cilindro ocupa.
Esses conceitos são fundamentais em geometria e têm aplicações práticas em diversas áreas, como engenharia, física e matemática aplicada.
Valor de Pi
Valor da circunferência
Volume do cilindro (Área da base x altura)
Resumo com mapa mental
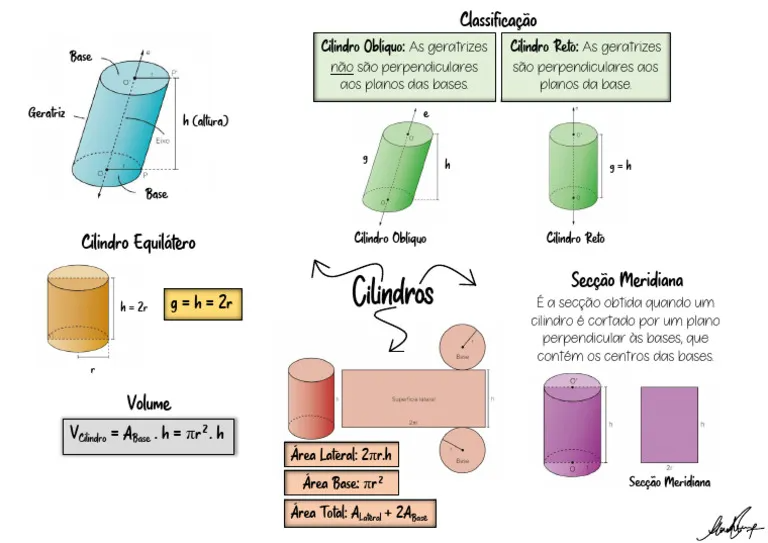
Elementos de um cilindro
Quais são os elementos do cilindro?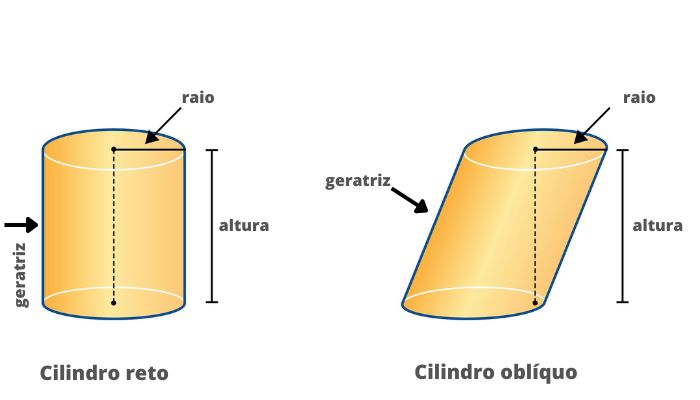
Elementos de um cilindro reto e de um cilindro oblíquo.
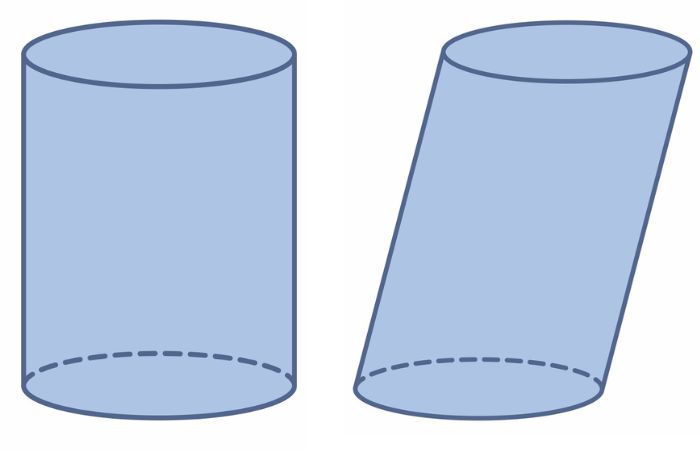Cilindro reto e cilindro oblíquo, respectivamente.
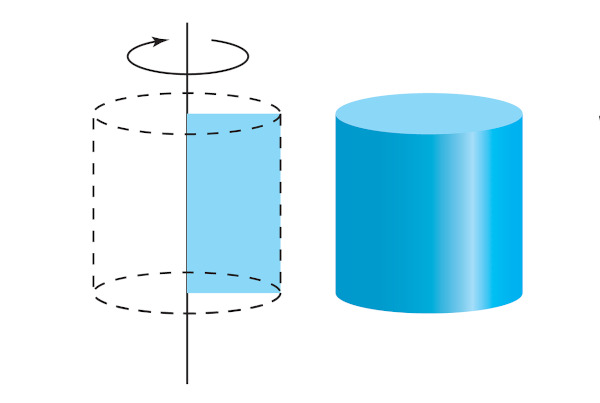Revolução de um retângulo na formação do cilindro reto.
Elementos de um cilindro reto e de um cilindro oblíquo.
- Bases: as bases do cilindro são os dois círculos presentes na superfície do cilindro, um na parte superior e outro na parte inferior.
- Altura: a altura do cilindro é a distância entre os planos que contêm suas bases.
- Geratriz: geratriz do cilindro é a medida de um segmento com extremidades nas circunferências das bases e paralelo ao eixo central (que liga os centros das bases).
Cilindro reto e cilindro oblíquo, respectivamente.
- Cilindro reto (ou cilindro de revolução): se a geratriz de um cilindro é perpendicular aos planos das bases, o cilindro é classificado como reto ou de revolução, pois resulta da revolução de um retângulo. No cilindro reto, a altura e a geratriz possuem a mesma medida.
Revolução de um retângulo na formação do cilindro reto.
- Cilindro oblíquo: se a geratriz de um cilindro não é perpendicular aos planos das bases, o cilindro é classificado como oblíquo. Nesse caso, a altura e a geratriz têm medidas diferentes.
- r → raio do círculo (raio da base).
1) Seja um cilindro de 20 cm de altura e raio da base de 5 cm. Calcule o volume do cilindro.
2) Uma lata de óleo tem uma base de 8 cm de diâmetro e 19 cm de altura.
Unidades de medida e unidades de medida de capacidade
As medidas de capacidade representam as unidades usadas para definir o volume no interior de um recipiente. A principal unidade de medida da capacidade é o litro (L).
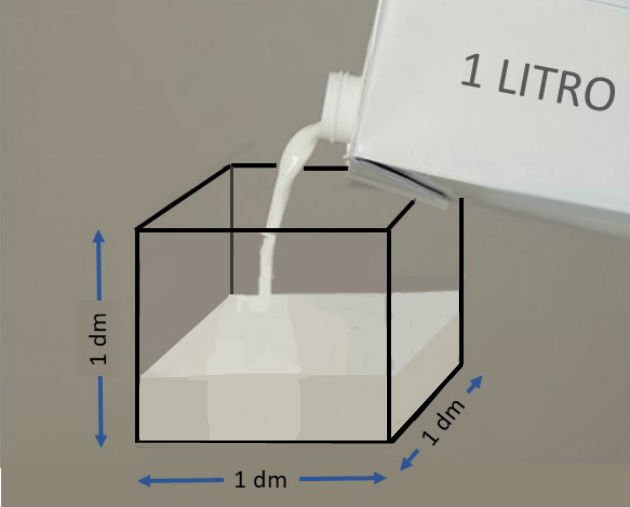
O litro representa a capacidade de um cubo de aresta igual a 1 dm. Como o volume de um cubo é igual a medida da aresta elevada ao cubo, temos então a seguinte relação:
1 L = 1 dm3
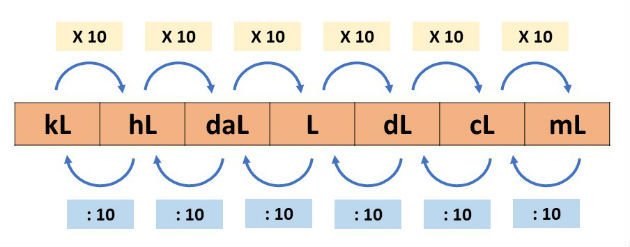
Mudança de UnidadesO litro é a unidade fundamental de capacidade. Entretanto, também é usado o quilolitro(kL), hectolitro(hL) e decalitro que são seus múltiplos e o decilitro, centilitro e o mililitro que são os submúltiplos.
Como o sistema padrão de capacidade é decimal, as transformações entre os múltiplos e submúltiplos são feitas multiplicando-se ou dividindo-se por 10.
Para transformar de uma unidade de capacidade para outra, podemos utilizar a tabela abaixo:
Mudança de UnidadesO litro é a unidade fundamental de capacidade. Entretanto, também é usado o quilolitro(kL), hectolitro(hL) e decalitro que são seus múltiplos e o decilitro, centilitro e o mililitro que são os submúltiplos.
Como o sistema padrão de capacidade é decimal, as transformações entre os múltiplos e submúltiplos são feitas multiplicando-se ou dividindo-se por 10.
Para transformar de uma unidade de capacidade para outra, podemos utilizar a tabela abaixo:
Medida de Volume
As medidas de volume representam o espaço ocupado por um corpo. Desta forma, podemos muitas vezes conhecer a capacidade de um determinado corpo conhecendo seu volume.
A unidade de medida padrão de volume é o metro cúbico (m3), sendo ainda utilizados seus múltiplos (km3, hm3 e dam3) e submúltiplos (dm3,cm3 e mm3).
Em algumas situações é necessário transformar a unidade de medida de volume para uma unidade de medida de capacidade ou vice-versa. Nestes casos, podemos utilizar as seguintes relações:
- 1 m3 = 1 000 L
- 1 dm3 = 1 L
- 1 cm3 = 1 mL
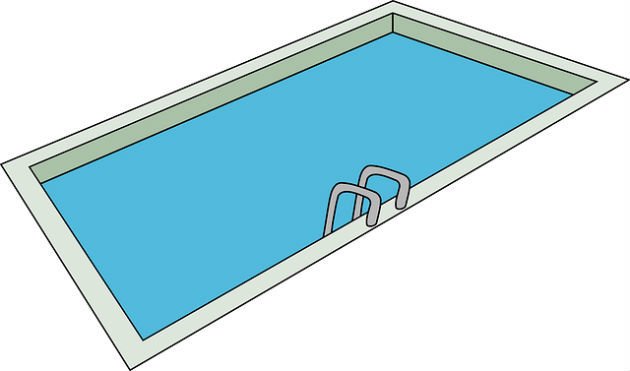
3) Volume da piscina
A piscina, representada na imagem abaixo, possui as seguintes dimensões: 7 m de comprimento, 4 m de comprimento e 1,5 m de altura. Quantos litros de água serão necessários para que a esta piscina fique completamente cheia?
4) Uma garrafa térmica com capacidade de 1,5 l (litros) será utilizada para servir café aos participantes de uma reunião. A bebida será servida em xícaras de 60 ml (mililitros). Determine a quantidade de xícaras que poderão ser servidas.
5) Uma piscina com a forma de paralelepípedo possui 30 m³ (metros cúbicos) de volume. As medidas de comprimento, largura e altura da piscina são, em metros, 5 m, 3 m e 2 m, nesta ordem. O volume da piscina em decímetros cúbicos é de:
6) transforme 57 dm³ (decímetros cúbicos) em cm³ (centímetros cúbicos).
Observando a tabela de múltiplos e submúltiplos do m³ (metro cúbico), verificamos que o centímetro cúbico está uma coluna à direita. Assim, avançamos com a vírgula três "casas" para a direita.
Múltiplos Medida base Submúltiplos.
Na prática, a cada coluna à direita, multiplicamos por 1 000.
Assista para responder a questão 7
Análise da das medidas
Para encontrar as medidas reais do personagem Jerry, do desenho "Tom e Jerry", e comparar essas dimensões com objetos do mundo real, como uma caneta e uma piscina, precisamos fazer algumas estimativas baseadas em observações dos episódios.
Estimando as Medidas do Jerry Vamos assumir que Jerry é um rato comum, cujas dimensões com comparação com uma caneta esferográfica típica tem as seguintes dimensões:
Análise da altura de Jerry
Usando uma régua, podemos comparar a altura de Jerry (10 cm) com o comprimento de uma caneta (12 cm).
Análise da altura da piscina e das marcações laterais
Dimensões de uma Piscina
Agora, vamos considerar uma piscina retangular padrão para a comparação. Suponhamos que Jerry aparece próximo a uma piscina em um dos episódios, e estimamos que ele tenha 10 cm de comprimento.
Vamos considerar uma piscina de dimensões típicas:
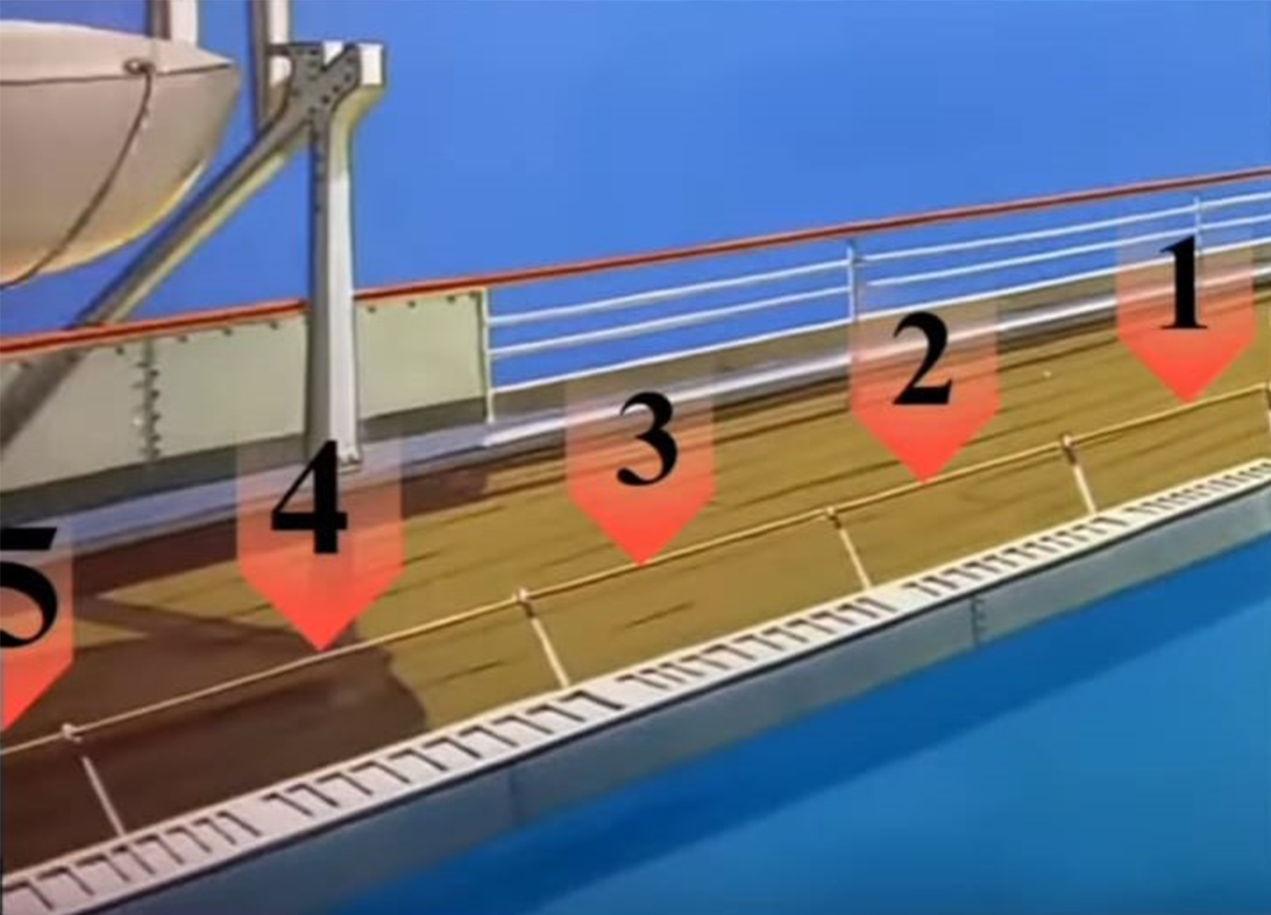Marcações laterais
Observando as marcações da bandeira e criando uma projeção podemos aproximas das medidas
Projeções das laterais
Análise da altura de Jerry
Usando uma régua, podemos comparar a altura de Jerry (10 cm) com o comprimento de uma caneta (12 cm).
Análise da altura da piscina e das marcações laterais
Dimensões de uma Piscina
Agora, vamos considerar uma piscina retangular padrão para a comparação. Suponhamos que Jerry aparece próximo a uma piscina em um dos episódios, e estimamos que ele tenha 10 cm de comprimento.
Vamos considerar uma piscina de dimensões típicas:
- Comprimento
- Largura
- Profundidade média
Marcações laterais
Observando as marcações da bandeira e criando uma projeção podemos aproximas das medidas
Projeções das laterais 7) Sabendo as dimensões da piscina, qual volume de água em litros?
8) Duas latas personalizadas foram projetadas com dimensões diferentes. A primeira lata tem formato cilíndrico, com um diâmetro de 10 cm e altura de 12,5 cm. A segunda lata também é cilíndrica, porém com um diâmetro de 8 cm e altura de 14 cm. Para determ
Qual das duas latas tem o maior volume?
Justifique sua resposta apresentando:
a) Calcule o volume da primeira lata.
b) Calcule o volume da segunda lata.
c) Qual das duas latas tem o maior volume?