Google ClassroomGoogle Classroom
GeoGebraGeoGebra Classroom
GeoGebra

De top van een parabool, deel 1

Author:Pieter Mijnhout

Welkom!

Welkom in dit werkblad over de top van een parabool. In dit werkblad ga je leren hoe je de coördinaten van de top van een parabool kunt berekenen vanuit drie verschillende vormen van een kwadratische functie. Tijdens het doorlopen van dit werkblad zal je berekeningen moeten maken waar je pen en papier voor nodig hebt. Veel plezier en succes!
Een kwadratische functie in de vorm f(x) = ax2+bx+c

Vraag 1.1

Gegeven is de functie Met de vergelijking  kan je de snijpunten van de grafiek met de x-as berekenen. Waarom is dat zo?

Tick all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Vraag 1.2

Los de vergelijking  op. Wat zijn de coördinaten van de snijpunten met de x-as?

Tick all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

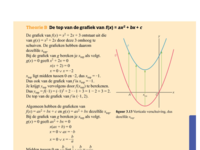
Hieronder zie je de grafiek van f

Vraag 1.3

Kloppen de berekende coördinaten van de snijpunten met de x-as?

Tick all that apply
  • A
  • B
Check my answer (3)

Vraag 1.4

Lees in de grafiek af wat het x-coördinaat van de top van de parabool is

Tick all that apply
  • A
  • B
Check my answer (3)

Vraag 1.5

Hoe had je dit kunnen berekenen zonder de grafiek te bekijken?

Tick all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Lees de theorie over de top van een parabool

Theorie Xtop.pdf

Theorie Xtop.pdf

Info

De algemene vorm voor een kwadratische functie is . Uit de theorie hierboven blijkt dat het x-coördinaat van de top berekend kan worden met , waarin de en de voor getallen uit de functie staan.

Vraag 1.6

Hoe ziet de berekening er uit om het x-coördinaat van de top van de parabool met functie te berekenen?

Tick all that apply
  • A
  • B
  • C
Check my answer (3)

Vraag 1.7

Voer de berekening van vraag 1.6 uit. Kom je op deze manier op hetzelfde antwoord als bij Vraag 4?

Tick all that apply
  • A
  • B
Check my answer (3)

Opdracht

Hieronder zie je nogmaals de grafiek met de functie Met de schuifknoppen kan je functie f en daarmee de parabool aanpassen. Verander de functie f met de schuifknoppen tot je de functie krijgt.

Vraag 1.8

Bereken met  het x-coördinaat van de top van de nieuwe parabool en controleer je antwoord met behulp van de grafiek

Vraag 1.9

Verander nu de schuifknoppen in willekeurige getallen. Bereken voor een willekeurige nieuwe situatie het x-coördinaat van de top van de parabool. Controleer je antwoord met behulp van de grafiek. Schrijf hieronder op welke functie je hebt gemaakt en wat het x-coördinaat van de top is.

Vraag 1.10

Waarom zit er geen in de berekening voor de ?

Tick all that apply
  • A
  • B
  • C
Check my answer (3)

Vraag 1.11

Je hebt nu van meerdere parabolen het x-coördinaat van de top berekend. Dit kan op een snelle manier met . Hoe kan je het y-coördinaat van de top van een parabool berekenen?

Tick all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Vraag 1.12

Voor de functie met kan je bereken door uit te rekenen. Wat zijn de coördinaten van de top (T) van de parabool?

Tick all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Gefeliciteerd!

Goed gedaan! Je hebt de coördinaten van de top berekend! Op naar de volgende vorm van een kwadratische functie. Open werkblad "De top van een parabool, deel 2"

New Resources

Discover Resources

Discover Topics