Dürer 2
On the next page of his book Dürer draws an ellipse correctly by elongating a circular arc.
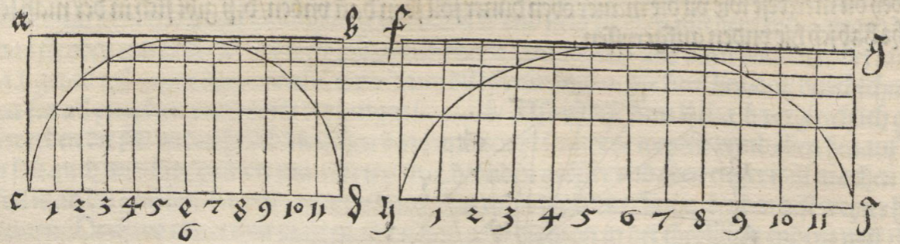
But, he doesn't know it's an ellips...
We have to wait until 1640 when Paul Guldin (1577-1643), een Swiss Jezuit, mathematician and astronomer who had contacts withJohannes Kepler, proved that an elongatet circle is an ellipse.
construction
- Draw a semi circle within the rectangle ABCD.
- Draw vertical lines and decide the rectangle in twelve equal parts.
- Adjacent to the ractangle ABCD draw a second rectangle EFGH, longer than the first one and devide it as well into 12 equal strokes.
- Define the intersection points of the circle and the vertical lines and draw horizontal lines through these intersection points.
- In rectangle EFGH define the intersection points of the horizontal and the vertical lines and connect them by a continuous curve.