Integration counter-examples : Witch's hat functions
What is this ?
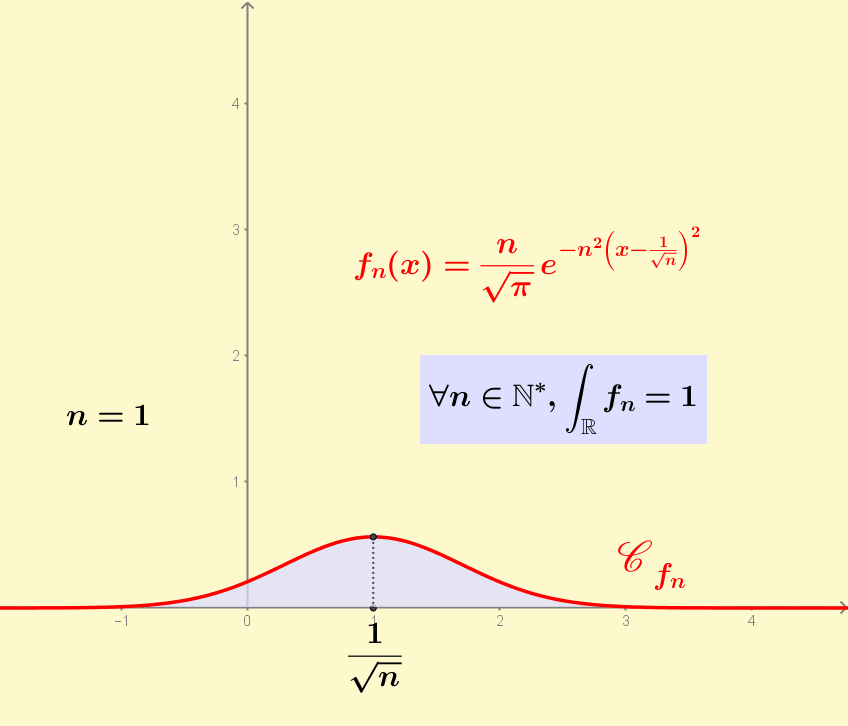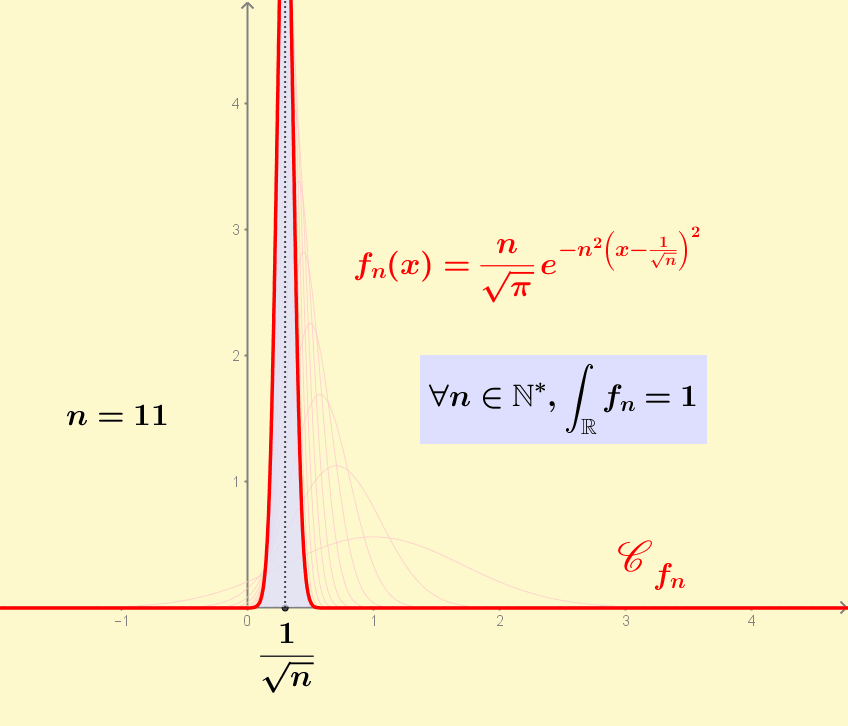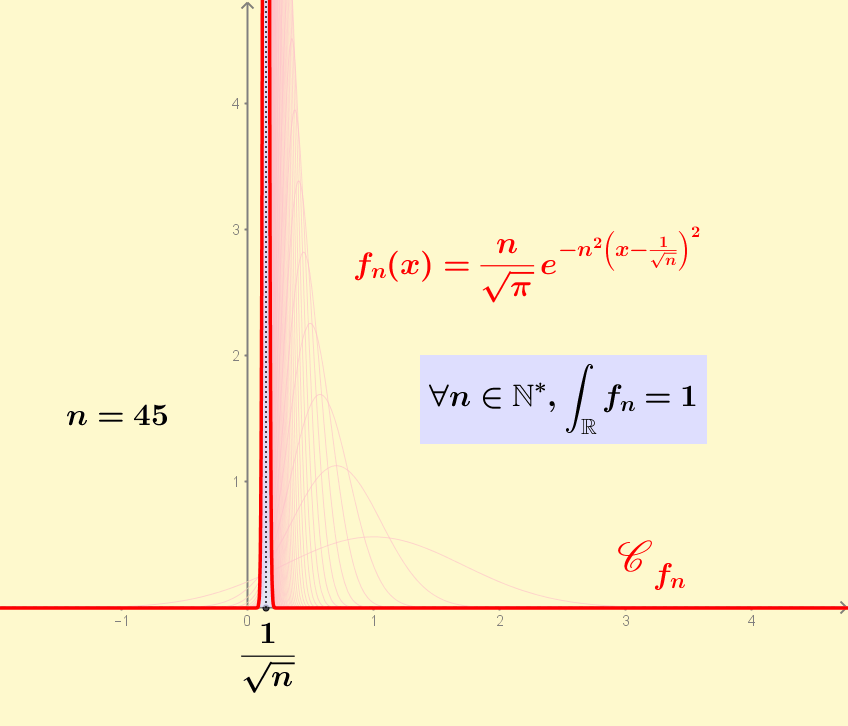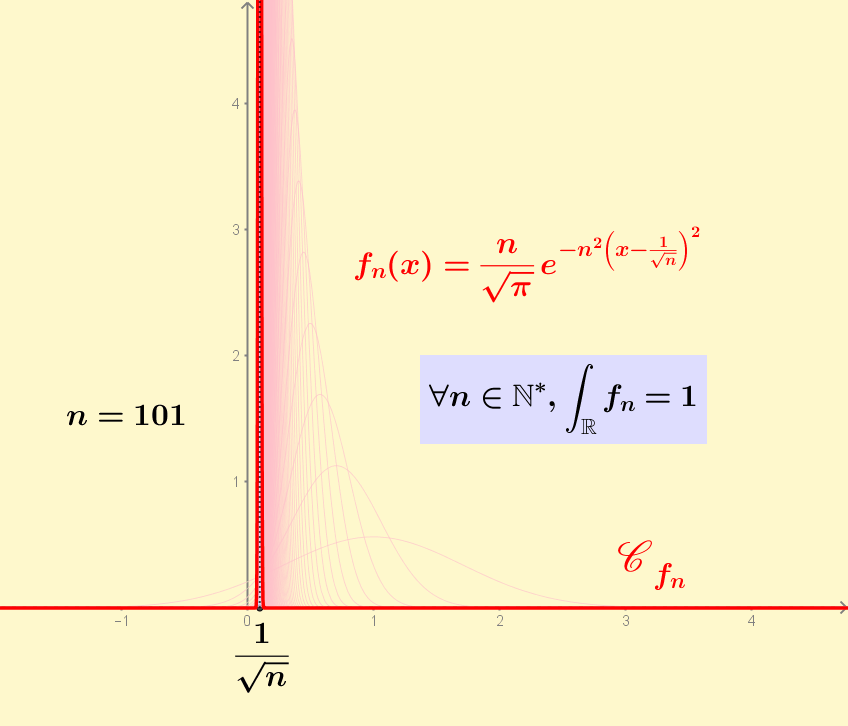
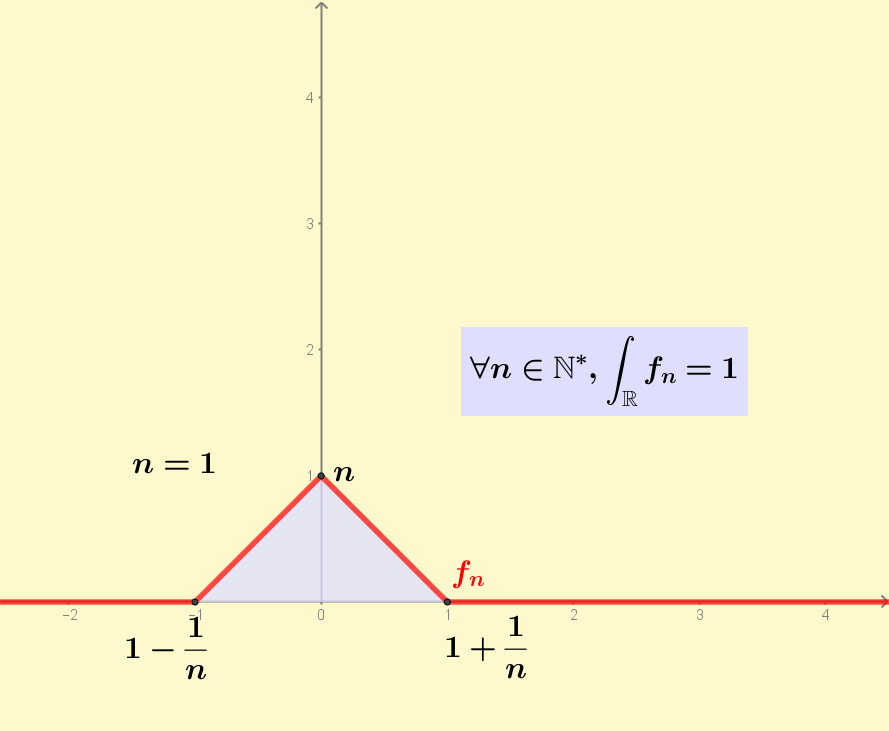
The functions f_n are continuous, converge pointwise almost everywhere to 0 as n goes to infinity and their integral is constant, equal to 1. So you cannot swap lim and integral when calculating the limit of the integral of f_n.
Animated GIF
Animated GIF version 2. Here the peak is not always in zero, but in 2/n. So the pointwise convergence of f_n to zero is for every point.
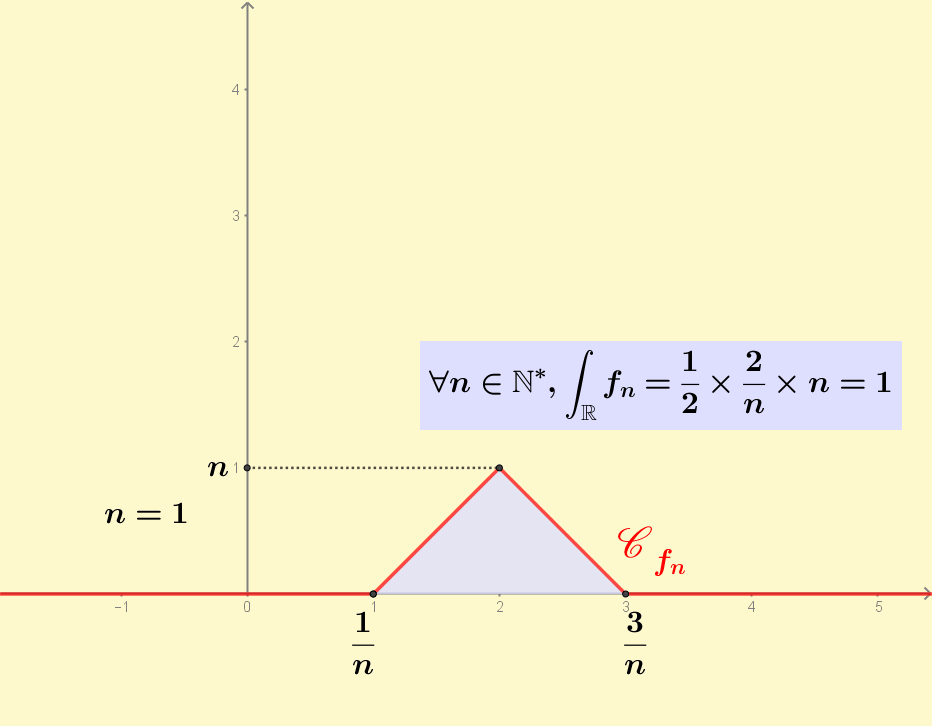
Version 2 with a moving peak in 2/n instead of 0.
You can use the same idea to construct a continuous non negative function whose integral converges although the function does not converge to zero. Here it was made so that there is a triangular bump for each positive integer n which has an area of 1/n².
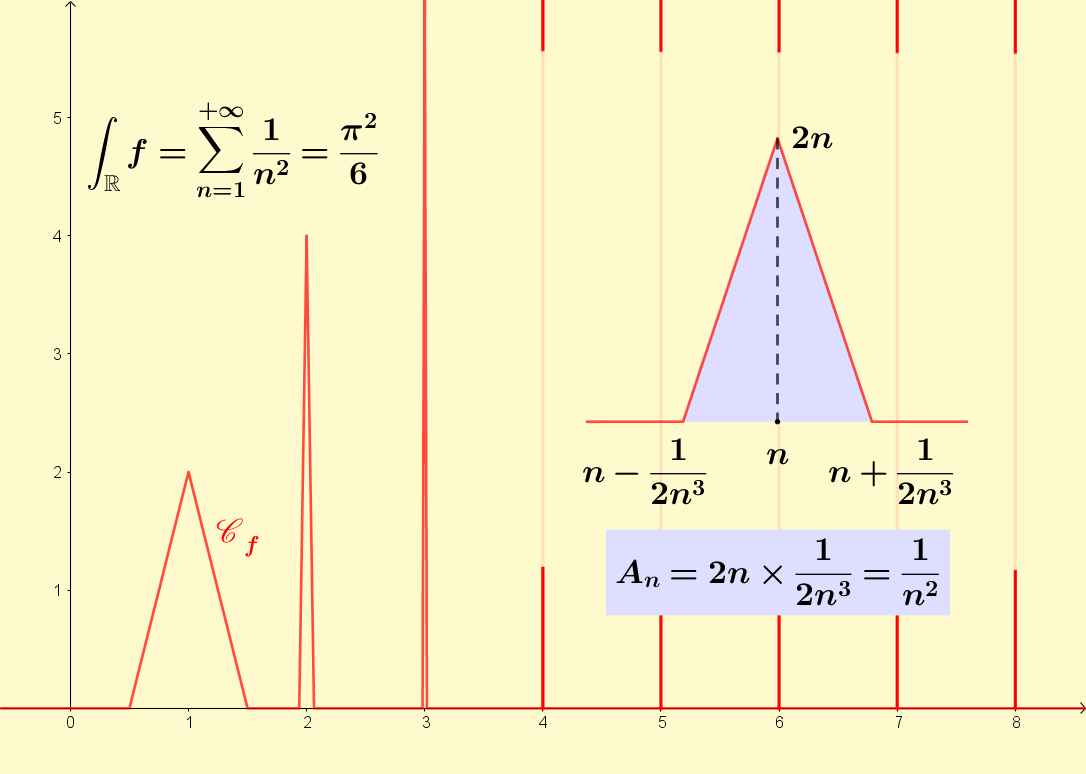
GIF animation of infinitely smooth functions fn converging pointwise to 0 (as all its derivatives) with integrals equal to 1 for all n.