Segmentos comensuráveis

Consideremos um segmento de reta AB. Para determinar a medida desse segmento, ou seja, a distância entre os pontos A e B, devemos fixar uma unidade de medida padrão u, denominada segmento unitário ou segmento de medida 1. Dividindo o segmento AB em n segmentos justapostos, com (n − 1) pontos interiores, a medida de AB será a soma das medidas desses n segmentos. Caso estes n segmentos sejam todos congruentes a u, então AB = n, isto é, u cabe n vezes em AB. Contudo, pode ocorrer de u não caber um número inteiro de vezes em AB. Neste caso, a medida de AB não será dada por um número inteiro positivo, o que conduz à definição de número racional ou fração. Para tanto, consideremos um segmento de reta r que caiba n vezes em u e m vezes em AB. Assim, o segmento r será uma medida comum de u e AB, estes denominados segmentos comensuráveis, isto porque existe uma unidade comum para expressar a medida de ambos. Desta forma, temos que r = e, consequentemente, AB = . Segundo Lima et al. (1997, p. 63): “Quando o segmento considerado é comensurável com a unidade escolhida, sua medida é um número racional (inteiro ou fracionário)”. A figura a seguir ilustra segmentos comensuráveis.

Segmentos não comensuráveis são denominados incomensuráveis. Neste caso, os segmentos não podem ser medidos com base em outra unidade de medida, como ilustra a figura abaixo.

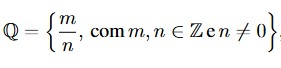
abrangendo os números naturais () e os números inteiros (). Nesta perspectiva, é importante destacarmos que existem diversas maneiras de definir os números racionais. De acordo com Charalambous e Pitta-Pantazi (2007 apud Quaresma; Ponte, 2012, p. 40), podemos relacionar cinco significados diferentes para os números racionais: (i) parte-todo – caso em que existe uma comparação entre a parte de um todo contínuo ou discreto, ou seja, o número racional representa a relação entre o numerador que indica o número de partes que se tomam do todo e o denominador que é o número de partes em que o todo está dividido, a compreensão deste significado é fundamental para a compreensão dos restantes significados; (ii) razão – designa uma comparação entre duas quantidades da mesma natureza ou de natureza distinta; (iii) operador – transforma o cardinal de um conjunto discreto, pode ser partitivo (no caso da fração ) ou multiplicativo partitivo (no caso da fração , com a0); (iv) quociente – um número racional visto como resultado de uma divisão entre dois números naturais, onde o numerador e o denominador representam o todo; (v) medida – situação que se traduz na comparação entre duas grandezas, em que uma delas é considerada a unidade. Assim, um número racional é representado por uma fração, a qual corresponde a um número inteiro ou a um decimal finito ou a uma dízima periódica. Ainda, podemos representar um número racional por meio de recursos gráficos, como ilustrações e retas numéricas. O número racional cinco décimos (que significa a metade de 1 inteiro), por exemplo, pode ser representado pela fração irredutível e pelo número decimal 0, 5, conforme as figuras abaixo.