T-Kreis mit TI Nspire
Mit TI Nspire kann man die Ortslinie erzeugen und mit 5 Punkten darauf den Kegelschnitt konstruieren.
Man kann dessen Gleichung angeben lassen.
Variiert man Punkte, ändert sich scheinbar die Gleichung des Kegelschnitts.
Aber bei allen Koeffizienten in gleicher Weise, so dass es für A = (0, 0) und B = (10, 0) letztlich immer um die Gleichung 0.1x² - x + y = 0 geht. Das ist eine Parabelgleichung.
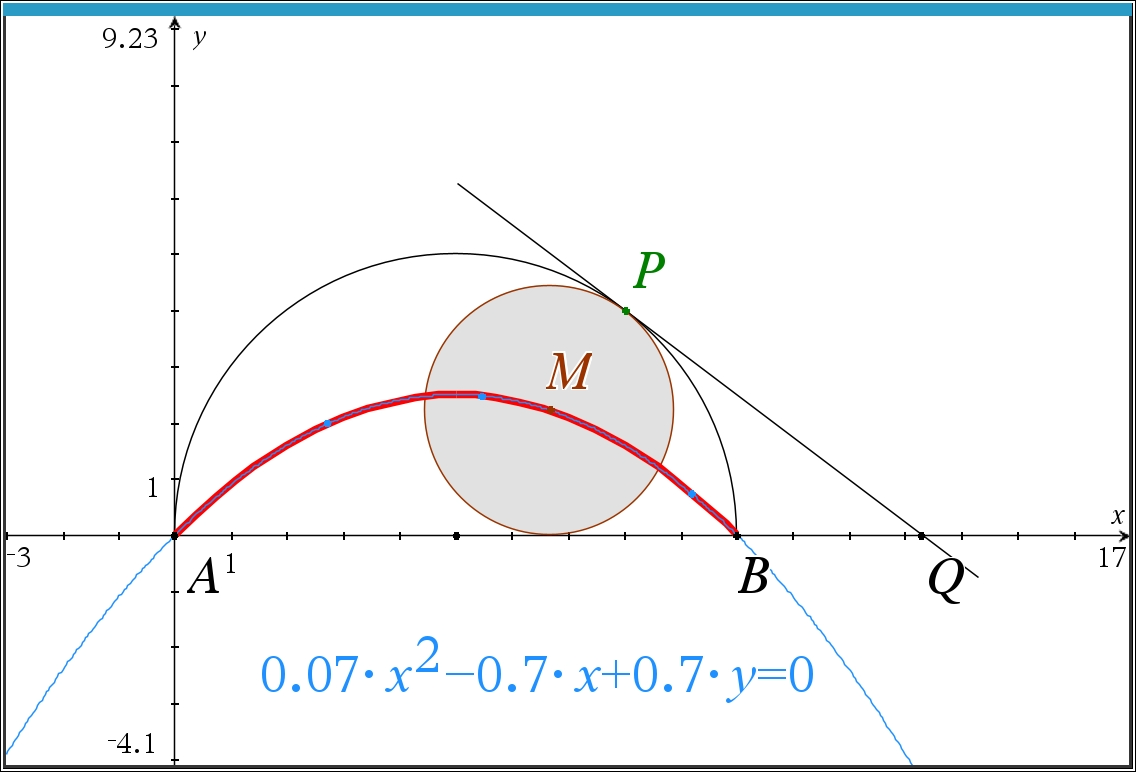
Das Geometriemodul vom Nspire basiert auf Cabri II. Deswegen ist es nicht überraschend, dass die Stabilität von Cabri II hier auch zu finden ist.