Osnova
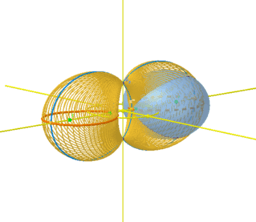
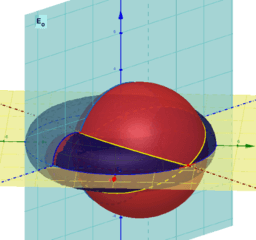
Darboux Cycliden & Bizirkulare Quartiken
Welcher Zusammenhang besteht zwischen
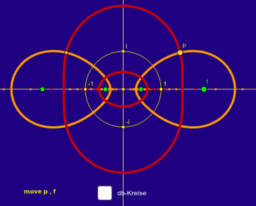
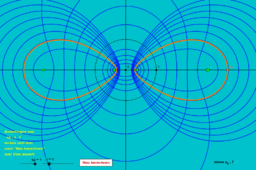
* bizirkularen Quartiken
und
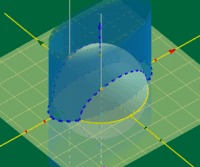
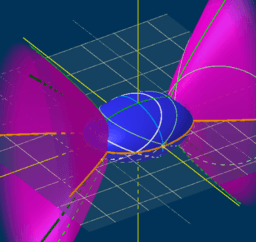
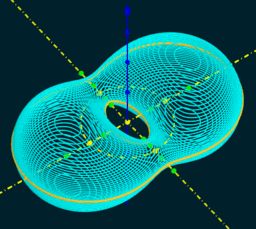
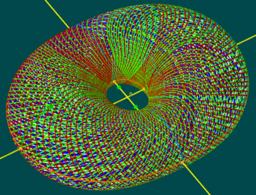
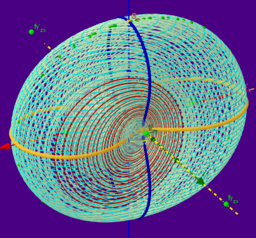
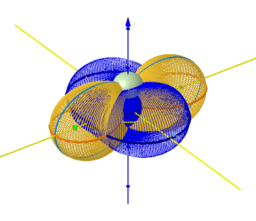
* DARBOUX Cycliden?
Eine Übersicht aus möbiusgeometrischer Sicht.
Kurz-Zusammenfassung:
Eine bizirkulare Quartik ist eine ebene Kurve 4. Ordnung des Typs:
- mit linearem und quadratischem und reellen Koeffizienten.
- mit linearem und quadratischem und reellen Koeffizienten.