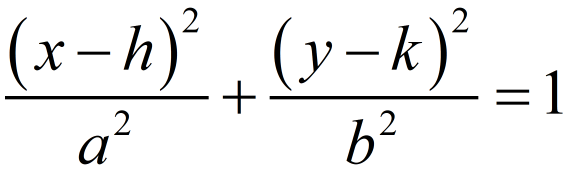La Elipse Actividad 4
INICIO
Usa la gráfica anterior, para realizar las acciones indicadas y responder las preguntas correspondientes.
1º Desplaza el punto Q libremente, y observa el valor de las sumas de distancias a dos puntos fijos F1 y F2 que está calculado en la parte superior.
¿Esta suma de distancias puede tomar cualquier valor?
Determina cuál es el valor mínimo de esta suma e indica la posición del punto.
¿Esta suma de distancias puede tomar cualquier valor?
Determina ¿Cuál es el valor mínimo de esta suma? e indica la posición del punto.
Al variar las posiciones de este punto P se obtiene la ELIPSE. Defínela como lugar geométrico.
¿Tiene algún tipo de simetría la elipse? ¿por qué?
¿Qué cumplen los puntos que no están situados en la elipse?
Determina el valor de a (SEMIEJE MAYOR) en función del valor de la suma de distancias de los puntos de la elipse a los focos. (Para justificarlo puedes situar el punto P sobre A)
¿Qué relación hay entre a, b y c? . (Para justificarlo puedes situar el punto P sobre B)
Determina el valor de b (SEMIEJE MENOR) en función de a y c.
DESARROLLO
La proporción o cociente entre c y a se llama EXCENTRICIDAD, e = c/a Si mantenemos el valor de a=5 , observa al modificar el valor de b, con el deslizador situado en la parte inferior derecha, observe cómo varían los focos y la forma de la elipse para responder las siguientes preguntas:
¿Qué ocurre cuando a=b?
¿Entre qué valores varía la excentricidad?
¿Qué interpretación podemos dar a la excentricidad?
Para el caso anterior, escribe la ecuación obtenida y el valor de a y b usados.
¿Qué sucede si a<b?
¿Qué sucede si a>b?
CIERRE
Las elipses vistas hasta ahora estaban centradas en el origen de coordenadas, la ecuación vista es la forma canónica. 6ºSi desplazamos la elipse situando el centro con los deslizadores situados en la parte inferior izquierda, se mantienen sus valores característicos a, b, c, e y sus relaciones. Los vértices y focos habrán sido desplazados. Compruébalo en diferentes casos y observa su ecuación.
¿Qué sucede si a=b?