Polar coordinate system, Archimedean spiral
The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.
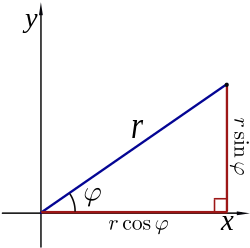
Converting between Polar and Cartesian coordinates:
Task:
The curve is given by polar equation r = 2+2cos φ. Determine the point with minimal curvature.
First, rewrite polar coordinates to the cartesian coordinates. Instead of the greek letter φ, we can use the letter t.
x = (2+2cos t).cos t
y = (2+2cos t).sin t
Task:
The curve is given by polar equation r = 2+2cos φ. Determine the point with minimal curvature.
First, rewrite polar coordinates to the cartesian coordinates. Instead of the greek letter φ, we can use the letter t.
x = (2+2cos t).cos t
y = (2+2cos t).sin tDetermine the point with minimal curvature (= krivost) on cardioid.
Archimedean spiral
Start the animation of revolving parameter a (left down corner). Value of slider u specify the position of osculating circle (red).
Stop the animation and set up the trace on for osculating circle. Then change the value of parameter u on red slider.