Example on max/min functions
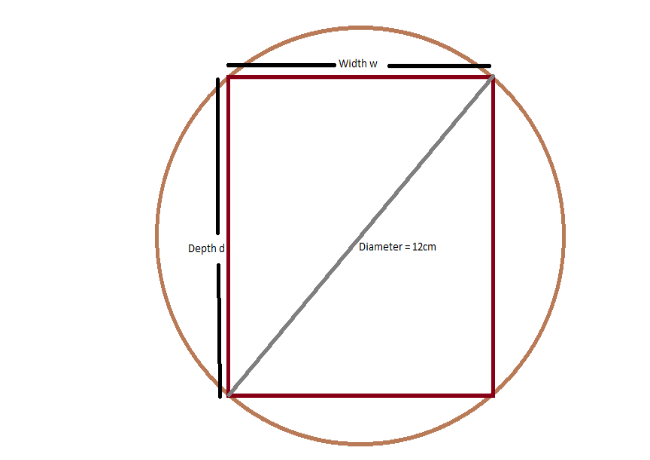
The strength of a wooden beam is given by , where depends on the type of wood(that is for a given type of wood k is a constant). What is the strongest beam that can be cut from a log with diameter 12cm?
The function provided by the exercise has two variables (width w and depth d), but to apply our Calculus methods, we need to transform it into a function of a single
variable. Knowing the beam will have a rectangular base, we can use
Pythagoras' theorem to find as a function of .
.
Substituting the value in S we get , and its derivative
Now that we have expressed the strength as a function of one variable w, the next step is to find the maximum values of the function on the interval .
The graph below shows in green and its derivative in orange, use them to find the maximum of the function S on (use an approximation if necessary). At what value w does this maximum occur?
Adjust the sliders in the diagram below to compare the value of the strength of the beam found by finding the values of w that minimise or maximise the function S with strengths at other values of and .
Is it possible to find other values for and , on that interval, that create a stronger beam?