Las lunas de Hipócrates

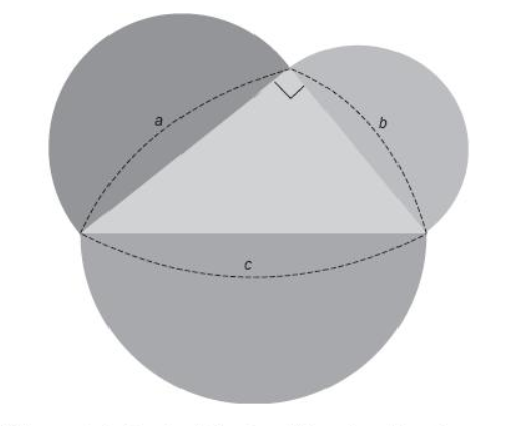
1. ¿Qué puedes decir acerca de la suma de las áreas de los semicírculos construidos sobre los catetos del triángulo rectángulo comparada con el área del semicírculo construido sobre la hipotenusa? Expresa tu hallazgo con palabras.

El diámetro de cada semicírculo es congruente con el lado correspondiente del triángulo. ¿Cuál es el radio de cada uno de los semicírculos sobre los lados del triángulo rectángulo? 1. Escribe el radio del semicírculo sobre el lado a

2. Radio del semicírculo sobre el lado b

3. Radio del semicírculo sobre el lado c

4. ¿Cuál es el área del círculo de radio ?

5. ¿Cuál es el área de un semicírculo de radio ?

6. Escribe una expresión algebraica para cada una de las áreas de los semicírculos. Área del semicírculo sobre el lado a

7. Escribe una expresión algebraica para cada una de las áreas de los semicírculos. Área del semicírculo sobre el lado a

8. Escribe el área del semicírculo sobre el lado b

9. Escribe el área del semicírculo sobre el lado c

10. Usa notación algebraica para expresar la suma de las áreas de los dos semicírculos de radios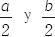 

11. Utiliza notación algebraica para expresar que la suma de las áreas de los semicírculos sobre los catetos a y b del triángulo rectángulo es igual al área del semicírculo sobre la hipotenusa c

12. Factoriza y simplifica ambos lados de la ecuación 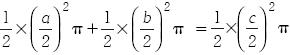 para mostrar que es equivalente a la ecuación a² + b² = c².

13. Puedes hacer esto en varios pasos. Puedes, por ejemplo, multiplicar ambos lados por 2 y dividir ambos lados entre π. Escribe la ecuación simplificada:

14. Ahora puedes expandir los términos cuadrados. Escribe la ecuación correspondiente:

15. Finalmente puedes multiplicar ambos lados por 4

16. Verifica que puedes invertir todos los pasos. Esto es, empieza con la ecuación a² + b² = c² y muestra paso a paso que, a partir de esta relación, puedes obtener la relación entre los semicírculos.  

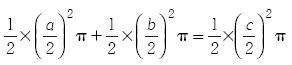
Mueve los puntos. Cambia de tamaño el triángulo rectángulo, mueve los puntos, forma polígonos distintos, cóncavos y convexos, y contesta: 1.¿Qué sucede con las áreas de los polígonos?

2.¿Se cumple el teorema de Pitágoras? Demuestrálo.

3. Escribe una regla general para el teorema de Pitágoras.