Geometria no círculo
Introdução
Ângulo ao Centro
Ângulo ao centro
Observa
Move o ponto D ao longo da circunferência e regista os valores da âmplitude do arco CD e do ângulo CAD. O que concluis?
Angulo inscrito
Diagrama
Compara
O que podes dizer sobre o ângulo CBD em relação ao arco CD?
Ângulo inscrito
Diagrama com amplitudes
Conclusões
Move o ponto B ao longo do arco CBD e repara na amplitude do ângulo CBD que obténs. Que concluis?
Conclusões
Move os pontos C e D para mudar a âmplitude do arco CD. Compara as amplitudes do ângulo CBD e do arco CD. O que concluis?
Para concluir
Completa a frase abaixo: "A amplitude do arco é o ____________ da amplitude do ________________"
Teorema do arco capaz
Compara
O que podes dizer sobre os ângulos CBD e CED em relação ao arco CD?
Compara
Move os pontos B e E ao longo do arco preto e regista as amplitudes dos ângulos CED e CBD. O que é que concluis em relação às amplitudes dos ângulos?
Completa
Completa a frase seguinte: "Ângulos opostos ao mesmo arco têm a _________ amplitude"
Exercícios de aplicação
Diagrama de um laço
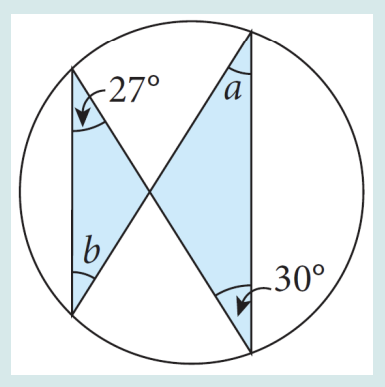
Observa a figura acima
Encontra o valor dos ângulos marcados com "a" e "b".
Triângulo retângulo com diâmetro de hipotenusa.
Recorre aos resultados anteriores para justificar este resultado.
Quadrilatero inscrito
Soma dos ângulos opostos de um quadrilatero inscrito numa circunferência
Na figura do exemplo 2 está representado um quadrilátero [ABCD] inscrito numa circunferência, com indicação da amplitude dos seus ângulos internos. Move os pontos A, B, C e D e observa como muda o valor dos ângulos internos do quadrilátero [ABCD]. Regista em cada caso o valor da soma dos ângulos opostos. O que concluis?
Justifica
Justifica a tua afirmação baseando-te nos resultados aprendidos antes.