Coniche: il cono infinito
Intersezionne Di un Piano con la superficie di un cono infinito. [Scuola secondaria I (3°Media) e II grado (I e II liceo)]
1) Costruisci uno Slider 
valore min 0 max 4.
2) Costruisci al volo in 3D il Punto
A=(2,0,0)
3 Costruisci la retta f 
perpendicolare al Punto A
4) Costruisci al volo 
il Punto B appartenente alla retta f.
5) Costruisci lo Slider α selezionando angolo Min 0° Max 50°.
6) Costruisci con inserisci lo script conoinfinito (B,A,α) inserendo i dati.
7) Costruisci in 3D sull'asse X la retta perpendicorare g al punto A.
8) Costruisci intersezione 
tra Cono e Retta g (Punti D e C).
9) Costruisci le due rette generatrici BD e BC 
del Conoinfinito.
10) Costruisci il Punto E Punto su un oggetto sulla retta BD.
11) Costruisci sulla retta i generatrice crea un segmento 
EF e nascondi la retta.
12) Costruisci Punto G sul segmento EF.
13) Costruisci due punti I e H al volo cercando di porli alla stessa quota sul Cono inferiore .
14) Costruisci il piano p per tre punti 
I,H,G.
15) Costruisci l'intersezione 
tra il Cono e il piano creato p.
16) Costruisci su Inserisci, con lo script fuoco e poi c (nome dell'ellisse).
17) In algebra sul punto G in basso a destra fai partire animazione per visualizzare le coniche generate in 2D
valore min 0 max 4.
2) Costruisci al volo in 3D il Punto A=(2,0,0)
3 Costruisci la retta f perpendicolare al Punto A
4) Costruisci al volo il Punto B appartenente alla retta f.
5) Costruisci lo Slider α selezionando angolo Min 0° Max 50°.
6) Costruisci con inserisci lo script conoinfinito (B,A,α) inserendo i dati.
7) Costruisci in 3D sull'asse X la retta perpendicorare g al punto A.
8) Costruisci intersezione tra Cono e Retta g (Punti D e C).
9) Costruisci le due rette generatrici BD e BC del Conoinfinito.
10) Costruisci il Punto E Punto su un oggetto sulla retta BD.
11) Costruisci sulla retta i generatrice crea un segmento EF e nascondi la retta.
12) Costruisci Punto G sul segmento EF.
13) Costruisci due punti I e H al volo cercando di porli alla stessa quota sul Cono inferiore .
14) Costruisci il piano p per tre punti I,H,G.
15) Costruisci l'intersezione tra il Cono e il piano creato p.
16) Costruisci su Inserisci, con lo script fuoco e poi c (nome dell'ellisse).
17) In algebra sul punto G in basso a destra fai partire animazione per visualizzare le coniche generate in 2D
ESEGUI QUI LA COSTRUZIONE
VERIFICA LA TUA COSTRUZIONE: MUOVI LA BARRA DI NAVIGAZIONE
Intersezionne di un Piano con la superficie di un cono infinito Scuola secondaria II grado
- Si consideri una retta a detta asse.
- Si consideri una seconda retta g detta generatrice che forma con a un angolo
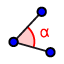. - Si ruoti g intorno ad a in modo da formare due falde coniche
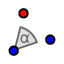
- Si consideri un piano π che forma con a un angolo
che taglia una o entrambe le f. coniche - La figura piana ottenuta intersecando il/i cono/i con il piano è detta conica.
- Un'ellisse possiede due sfere di Dandelin, entrambe tangenti alla stessa falda del cono.
- Un'iperbole ha due sfere di Dandelin che toccano le falde opposte del cono.
- Una parabola possiede una sola sfera di Dandelin.
![[justify][size=150][color=#ff0000]I fuochi dell'ellisse ottenuta intersecando
un cono con un piano, sono i punti di
contatto delle due sfere tangenti al piano
e tangenti (internamente) alla
superficie conica.[/color][/size][/justify]](https://www.geogebra.org/resource/szg84q7z/hbs1QMWNgEgj3DNf/material-szg84q7z.png)
I fuochi dell'ellisse ottenuta intersecando un cono con un piano, sono i punti di contatto delle due sfere tangenti al piano e tangenti (internamente) alla superficie conica.
AGISCI SULLE CASELLE DI CONTROLLO PER ESPLORARE LA COSTRUZIONE
Attività
Nell'attività interattiva di GeoGebra:
- Modifica l'inclinazione del piano variando l'angolo ed osserva nel piano quali figure si generano: in particolare individua la relazione fra l'angolo d'inclinazione del piano con l'angolo di apertura del cono in relazione alla conica che si genera nel piano, ovvero
- Per quali valori di si genera una circonferenza
- Per quali valori di e si genera un'ellisse
- Per quali valori di e si genera una parabola
- Per quali valori di e si genera un'iperbole
- Modifica l'apertura del cono variando l'angolo ed osserva nel piano quali figure si generano: in particolare osserva se si replicano le situazioni a., b., c. e d. del punto 1.
- Visualizza le sfere di Dandelin ed osserva quanto detto in teoria.
RISPONDI ALLE DOMANDE (3° media I e II Liceo)
La circonferenza si genera quando.
Le coniche ( ellisse, parabola e iperbole) si formano quando.