Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Grundlagen der Gewebelehre

Author:Walter Füchte

* * * z - Ebene → → → → w = tan(z) → → → → → → w - Ebene * * *

* * * z - Ebene → → → → w = tan(z) → → → → → → w - Ebene * * *

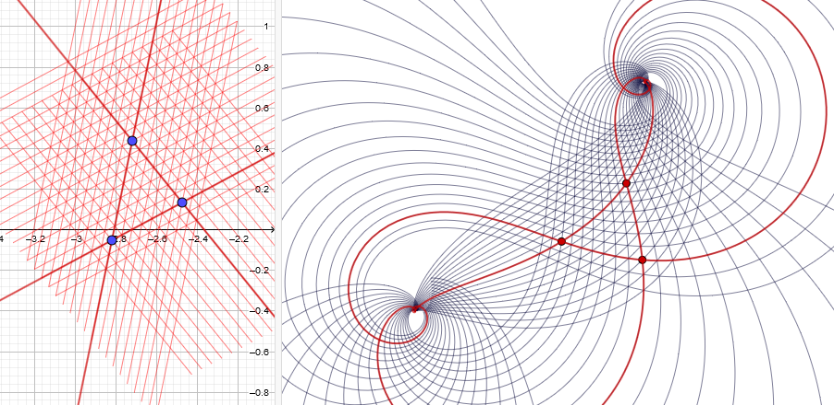
Dies ist ein Bild des Applets auf der vorigen Seite

Diese Seite ist Teil des GeoGebra-Books Moebiusebene. (Juli 2019)

Was ist ein Sechs-Eck-Netz oder (synonym) ein Sechs-Eck-Gewebe (manchmal auch Drei-Ecks-Netz)? Die folgende "Definition" ist nicht unter dem Aspekt größtmöglicher mathematischer Präzision, sondern mit dem Ziel formuliert, so weit möglich ein anschauliches Bild vom Sachverhalt zu entwerfen. Drei Kurvenscharen in einem offenen Gebiet der Ebene sollen die folgenden Eigenschaften aufweisen:
  • Durch jeden Punkt der Ebene geht aus jeder der drei Scharen genau eine Kurve.
  • Jede Kurve einer Schar schneidet jede einzelne Kurve einer der anderen Scharen in genau einem Punkt. (*)
Dann bilden die drei Kurvenscharen ein Sechs-Eck-Gewebe, wenn folgende Schließungsbedingung erfüllt ist:
Es sei irgendein Punkt des Gebiets und es seien , und die drei Kurven durch . sei irgendein ein 2.ter Punkt auf einer der drei Kurven, zB. auf . Die Kurven und durch schneiden , bzw. in den Punkten bzw. . Die Kurve durch schneidet in . Die Kurve durch schneidet in . Die Kurven durch und durch schneiden sich auf . Das Sechs-Eck schließt sich in diesem Schnitt-Punkt ! 
Die Frage, ob 3 Kurvenscharen in der Ebene ein Sechs-Eck-Gewebe bilden, ist einfach zu beantworten: Meistens nicht! Welche Methoden gibt es, Sechs-Eck-Gewebe zu erkennen? Die Methoden zum Nachweis für das Vorliegen eines Sechs-Eck-Gewebe sind erstaunlich vielfältig. Wir wollen sie hier aufzählen, teilweise ohne exakten Beweis. (*) Diese Bedingung ist für Netze aus Kreisen zu streng: Zwei Kreise können sich in 2 Punkten schneiden, sie können sich berühren (1 Schnittpunkt) oder sie können sich überhaupt nicht schneiden. Diese 3 Fälle liegen oft nahe beieinander! Die auf den folgenden Seiten angezeigten Beispiele von Sechs-Eck-Netzen aus Kreisen lassen die genannten 3 Fälle an den Rändern des Gültigkeitsbereiches gut erkennen. Drei Parallelenscharen in drei verschiedenen Richtungen bilden stets ein Sechseck-Gewebe. Dies sieht man leicht mit Hilfe der Vektorrechnung ein: Es sei eine der drei Parallelen-Richtungen. Die beiden anderen Richtungsvektoren , kann man so normieren, dass gilt. Dann wird das Sechs-Eck-Gewebe punktweise durch mit erzeugt. Die Parallelenscharen kann man beschreiben durch Funktionen , und mit reellen Koeffizienten, die man so wählen kann, dass gilt. Wir nennen diese Netze aus 3 Parallelenscharen im Folgenden öfters "Standard-Netze". Methode I: Bildet man die Parallelen eines Standard-Netzes in einem Gebiet der Ebene ab mit einem Diffeomorphismus, so bilden die Bildkurven ein Sechs-Eck-Netz. Besonders schön werden die Bilder mit konformen Abbildungen in der GAUSSschen Zahlenebene. Konforme Abbildungen sind komplex-differenzierbare oder meromorphe Funktionen, ohne Nullstellen der Ableitung in dem fraglichen Bereich; sie sind winkeltreu, d.h. die Winkel in einem Netz aus 3 Parallelen-Scharen bleiben unter der Abbildung erhalten. Die Abbildung eines Standard-Netzes mit solchen komplex-differenzierbaren Funktionen ist unserer Meinung nach ein besonders nützliches und schönes Hilfsmittel, um die geometrischen Eigenschaften dieser Funktionen zu erkunden. Oben und auf der Seite zuvor ist das Bild eines Standard-Netzes unter der komplexen -Funktion dargestellt. Es gilt auch die Umkehrung der obigen Aussage: Jedes Sechs-Eck-Gewebe ist das diffeomorphe Bild eines Standard-Sechseck-Gewebes aus drei Parallelen-Scharen, zumindest in einem geeigneten offenen Beeich der Ebene und sofern naheliegende Differenzierbarkeits- und Regularitätsbedingungen erfüllt sind.

Sechseck-6-Netz

Methode II: Sind drei Kurvenscharen implizit gegeben als Niveaulinien dreier reellwertigen Funktionen:
  • , und mit
so bilden die 3 Kurvenscharen ein Sechs-Eck-Gewebe, sofern die nötigen Differenzierbarkeits- und Regularitätsbedingungen erfüllt sind. Für drei Parallelenscharen haben wir solche Funktionen angegeben (siehe vor Methode I). Im Applet oben ist ein ganz besonderes Sechs-Eck-Netz zu sehen: Drei Geradenbüschel erzeugen stets ein Sechs-Eck-Netz. Dies ist für sich schon bemerkenswert: die euklidischen Streckungen der Ebene mit verschiedenen Zentren sind nicht vertauschbar, während Verschiebungen es sind (Vektoraddition!). Die Sechs-Eck-Bedingung muss also für 3 Geradenbüschel mit verschiedenen Zentren anders als für 3 Parallelenscharen begründet werden. Oben wird das Sechs-Eck-Netz obendrein ergänzt durch 3 Kegelschnittbüschel: die Kegelschnitte durch 2 der Zentren mit den Verbindungsgeraden zum 3. Zentrum als Tangenten. Je drei diese 6 Kurvenscharen bilden ein Sechs-Eck-Gewebe, die anderen 3 Kurvenscharen liefern die Diagonalen des Netzes. Ein Gewebe aus Kurvenscharen, von denen je 3 ein Sechs-Eck-Gewebe bilden, wird Sechseck-n-Gewebe genannt, siehe dazu das Buch [BLA_BO] "Geometrie der Gewebe" von W. BLASCHKE und G. BOL (1938) (Literaturverzeichnis). Oben liegt also ein Sechseck-6-Gewebe vor. Begründung (Kurzfassung): In geeigneten homogenen Koordinaten sind diese sechs Kurvenscharen Niveaulinien der Funktionen:
  • , , ;
  • und , ,
Das Verständnis von "homogenen Koordinaten" setzt ein wenig Vertrautheit mit projektiven Denkweisen voraus. Wir wollen das hier nicht vertiefen!
Methode III: Gibt es zu einem Gewebe aus drei Kurvenscharen eine Ein-Parameter-Gruppe von Abbildungen, für welche die Kurven von Bahnkurven sind und die Kurvensysteme als Ganzes festbleiben, so ist das Gewebe ein Sechs-Eck-Gewebe. Die oben genannten Voraussetzungen an die 3 Kurvenscharen mögen vorliegen.
Zur Begründung zeigen wir, dass sich jede Sechs-Eck-Figur schließt - zumindest im Kleinen. Es seien die 3 Kurven aus den 3 Scharen durch einen vorgegebenen Punkt , und es sei ein zweiter Punkt, etwa auf . seien die Bildkurven unter derjenigen Abbildung aus der Gruppe, für welche durch geht. Die Kurven bilden eine "Raute" mit den Schnittpunkten . Die Abbildung ergänzt das Sechs-Eck, die fehlenden 2 Kurven sind die Bahnkurven durch und .
Methode IV: Wieder liege ein Gewebe aus 3 Kurvenscharen mit den genannten Voraussetzungen vor. Zu jeder Kurve möge es eine 'Spiegelung' geben, d.i. eine involutorische Abbildung, welche punktweise festläßt. Wenn diese 'Spiegelungen' als Ganzes festlassen, und sie die beiden anderen Kurvenscharen vertauschen, dann bilden die 3 Scharen ein Sechs-Eck-Gewebe.
Begründung: Es seien wie oben die Kurven durch einen Punkt und ein weiterer Punkt, beispielsweise auf . Die Kurve durch schneide in . Die Kurve durch schneide in . Die Kurve durch schneide in . Die Spiegelung an ergänzt die Figur zur Sechseckfigur.
In den Applets oben und unten ist links ein Beispiel für die Methode III, und rechts eines für die Methode IV dargestellt. Die Bahnkurven sind links die Kreise des hyperbolischen Kreisbüschel um die beiden Grundpunkte, unten sind das 0 und , die Bewegungen sind die Drehungen um die Grundpunkte. Die Spiegelungen rechts sind die Spiegelungen an den hyperbolischen Kreisen. Die Schar der Berührkreise bleibt bei den Drehungen wie bei den Spiegelungen erhalten!
Methode V: Konstruktion mit drei Vektorfeldern Eine Kurvenschar aus differenzierbaren Kurven in einem offenen Gebiet derart, dass durch jeden Punkt genau eine Kurven mit nicht-verschwindender Ableitung geht, legt ein Vektorfeld in diesem Gebiet fest. Zu drei Kurvenscharen gehören, genügende Differenzierbarkeit vorausgesetzt, 3 Vektorfelder . Wenn man weiter voraussetzt, dass diese Kurven sich in dem offenen Gebiet nirgends berühren, so zeigen die Tangentialvektoren in jedem Punkt in 3 verschiedene Richtungen. In der Ebene sind 3 Vektoren linear abhängig, es muss daher möglich sein, durch geeignete differenzierbare Umnormierung mit differenzierbaren Funktionen zu erreichen, dass gilt:
Beschreibt man das Standard-Sechs-Eck-Gewebe der drei Parallelenscharen
  • , , durch die Vektorfelder , und
so ist die Bedingung erfüllt. Überdies gilt in diesem Falle: . Das LIE-Produkt zweier Vektorfelder ist dabei erklärt durch: . Es gelten die Regeln:
Kriterium: Ein Gewebe werde beschrieben durch die drei Vektorfelder mit . Das Gewebe ist genau dann ein SechsEck-Gewebe, wenn eine gemeinsame Umnormierung , existiert, so dass das LIE-Produkt verschwindet:
Wir wollen im Folgenden die Sechs-Eck-Gewebe aus Kreisbüscheln bestimmen. Dazu formulieren wir das Kriterium in einer uns nützlichen Form:
  • Für die Vektorfelder gelte in einem Gebiet
    • mit nirgends verschwindenden reellwertigen Funktionen ,
    • und es sei .
    Die Integralkurven bilden genau dann ein Sechs-Eck-Gewebe, wenn gilt:
Wir hatten die Infinitesimalen von Keisbüscheln als Vektorfelder gedeutet. Zwei Infinitesimale sind nur dann vertauschbar, d.h. ihr LIE-Produkt ist 0, wenn sie zu demselben hyperbolischen, bzw. parabolischen Kreisbüschel gehören. Es sei also z.B. ein hyperbolisches Kreisbüschel. Die Vektorfelder erfüllen das obige Kriterium, wenn nicht reell abhängig sind. Es handelt sich um ein Sechs-Eck-Gewebe aus Kurven, die die Kreise des hyperbolischen Kreisbüschels unter 3 verschiedenen Winkeln schneiden: das Deckblatt dieses geToolbar Imagegebra-books zeigt ein solches Sechs-Eck-Gewebe.

Diese Aktivität als PDF-Datei: Grundlagen der Gewebelehre - GeoGebra

Grundlagen der Gewebelehre - GeoGebra.pdf

Grundlagen der Gewebelehre - GeoGebra.pdf

New Resources

Discover Resources

Discover Topics