万華鏡(雪の結晶の続き)
このワークシートはMath by Codeの一部です。
アート、背景、実装、バリエーションの順に見ていきましょう。
万華鏡
雪の結晶の背景の続き
<壁紙群(Wallpaper groups)>
群論では、N個の要素の順列N!、これを操作とみたときの置換が作る群、対称群Snが基本になります。
対称群の要素にはきれいな入れ替えもありますが、なんでもありです。
とくにきれいな入れ替えは、正N角形の回転であるサイクル、巡回群Cnですね。
(例)
C3は正三角形の120度回転操作、{e,r,r^2}の3要素からなり、生成元はr(120度回転)です。
模様で大切なのは、
正N角形を裏返せる立体図形と考えると面が裏と表の2面あるため、奇妙ですが、2面体ともいえます。
そこで、回転だけの巡回群Cnに対称軸の裏返しもいれた2面体群Dnもきれいです。
(例)
D4は正四角形の90度回転と裏返し、{e,r,r^2,r^3, t, rt, r^2 t ,r^3 t}の 4×2=8要素からなります。
生成元はr(90度回転)とt(裏返し)の2つです。
壁紙の繰り返しのパターン(周期性、対称性)を17種類に分けられています。それが壁紙群です。
平行移動の他に鏡映移動や回転移動を含めて、その対称性からの分類になっています。
パターンの記号の主な意味は次の通りです。
・NはN回回転すると重なる模様で、360÷N(度)の回転対称性を表しています。
(例)
2は360÷2=180度、3は360÷2=120度、4は360÷4=90度、6は360÷6=60度ですね。
・mは鏡映(Mirror,reflection), gは映進(Glide reflection)の略です。
鏡映は鏡に映したように裏返すことですが、映進は裏返してずらす。
(例)
右手のマークのとなりに左手のマーク、次は右手のマークと交互に格子状になら別と鏡映ですが、
右足のマークのとなりはあけてその上に左足のマークというようにスライドすると映進です。
超ざっくりですが、
17種類の名前、例、(巡回群、2面体群での分類名)のリストです。
1.p1:平行移動だけ。ただの格子点など
2.p2: 半回転。千鳥格子など
3.pm:平行鏡映。ハートマークをたてよこにならべる
4.pg: 映進。ジグザグ矢印
5.cm: 鏡映、中心斜鏡映。対称図形の斜めスライド
6.pgg:複数映進。となりの列が映進、同じ列は平行移動。Sと逆さSの連続。
7.pmg:鏡映、映進、半回転対称性。上下左右に鏡映されたブロックが並ぶ
8.p4:直角回転。直角に交わる十字
9.p4m:直角回転、複数鏡映。となりの行・列のたて横が変わる格子模様。(D4)
10.p4g:直角回転、映進。格子状にねじれ模様
11.p3:120度回転。3方向に反復。正六角形のひし形分割と模様の回転(C3)
12.p3m1:120度回転、鏡映。 正3角形の回転分割を鏡映をするか、
正六角形を3等分したひし形パーツの1つ1つに鏡映がはいっている。万華鏡(D3)
13.p31m:120度回転、複数鏡映。正3角形の回転分割から鏡映つきの正六角形をつくる(C3,D3)
14.p6:60度回転。6方向に反復(C6)
15.p6m:60度回転、複数鏡映。正六角形を6等分したパーツの1つ1つに鏡映が入っている。
蜂の巣、雪の結晶、冒頭のアート(D6)
16.p2mm (pmm):垂直方向の鏡映。たて横回転のない普通の格子模様(D2)
17.p2mg (pmg):半回転、映進。ジグザグと回転の模様
2.実装
冒頭のアートは、正六角形の中にある直角三角形ABCを回転と、
正三角形ABCの斜辺だけが移動する裏返しが見えるようにしています。
これは雪の結晶と同じ壁紙群p6m(D6)のしくみになっていました。
また、図形の反復だけでなく、図形の中の折れ線の動きがどう反映されるかを感じてもらうために
折れ線を動かせるようにしています。
質問:geogebraで模様つきの直角三角形ABCを敷き詰めるにはどうしたらよいでしょうか。
まず、直角三角形ABCをかきます。
「数式」が表示されていないときは、
メインメニューの「表示」で「数式」を選ぶと、数式が表示されて1行ずつ入力できます。
(0,0)と入れてエンターを押すと、A=(0,0)となります。
同様にして、B=(√3, 1), C=(√3,0)を入れましょう。(a=sqrt(3)としておくと、便利です。)
三角形ABCを作るにはpolygon(A,B,C)と入力します。勝手に名前がつくので、
たとえば、s=Polygon(A,B,C)とします。
三角形の辺上や内部に適当に点D,E,F,G,H,I,J,K,L,Mをとります。
t=polyline(D,E,F,G,H)
u=polyline(I,J,K,L,M)
とます。
zu= {s,t,u}
と入れると、zuという名前だけで、2本の折れ線が入った三角形ABCを呼び出せるのです。
zu2= Reflect(zu,y=0)がzuをx軸で鏡映したものです。
m1= Sequence(Rotate(zu,k*2*π/6, A), k,1,9)で、zuを60度回転した図列ができる。
m2= Sequence(Rotate(zu2,k*2*π/6, A),k,1,9)で、zu2を60度回転した図列ができる。
これをパックして、
kihon={m1, m2}
とすると、正6角形の基本図形kihonができました。
あとは、これを反復コピーしたリストを作ればよいですね。
点Bを点A(原点)を中心に反時計回りに60度回転した点、つまり、正六角形の頂点リストを作りましょう。これは、あとで図形の移動のために使いたいからです。
ptn=Sequence(Rotate(B,((2 π/6) k, A), k,1,6) とします。
次に、移動のための基本ベクトルを作りましょう。
Vector((a,0), (-a,0))がvになります。三角形の辺CAの2倍左に平行移動できますね。
kihon図形をv方向に‐3倍から3倍まで平行移動しましょう。
obi=Sequence(Translate(kihon,Vector(v k)),k,-3,3)
Vector(ptn(4),B)がwになります。
obiの行を選び、たて3点…のメニューから「入力の複製」を選びます。
コピーされた内容の「kihon」を「obi」に、ベクトルの[v]を[w]に変更すると、
敷き詰めができます。
l1=Sequence(translate( obi, Vector(w k)) ,k, -3, 3)
このように、kihonを作ってしまえば、
平行移動する方向移動ベクトルをA,B2つ決めることで、
obi= sequence( translate( kihon, Vector(A k)) ,k, -3, 3)
sequence(translate( obi, Vector(B k)) ,k, -3, 3)
と2段階の平行移動をするだけで敷き詰めが完了しますね。
そのあとの図1から図2もほとんど、同じやり方で作ってますので、
vectorの表示がオフになっているので、それをOnにしたり、図のsequenceのOnOffを
切り替えて作り方を確認してみよう。
そのときに、平行6辺形や平行4辺形への変更もイメージしてみよう。
3.バリエーション
今度は、この雪の結晶のしくみp6m(D6)を、万華鏡のしくみ(p3m1(D3))に改造してみよう。
質問:鏡映を正三角形の内部ではなく、ひし形の内部にして、回転を60度ではなく120度にした、万華鏡のしくみに改造するにはどうしたらよいでしょうか。
点A,Bはそのままにして、点Cの座標を(a,-1)にします。
三角形ABCは正三角形になりますね。
zu2の線対称の軸をx軸ではなく、y=-x/aにします。
m1,m2の回転角を2pi/6から、2pi/3にしましょう。
これで、kihonが正六角形になりますね。
あとの平行移動は冒頭のアートと何も変わりませんね。
万華鏡のしくみ
万華鏡p3m1や雪の結晶p6mのロジックで、
ランダムな模様を生成するアプリを作りたい。
<Python>
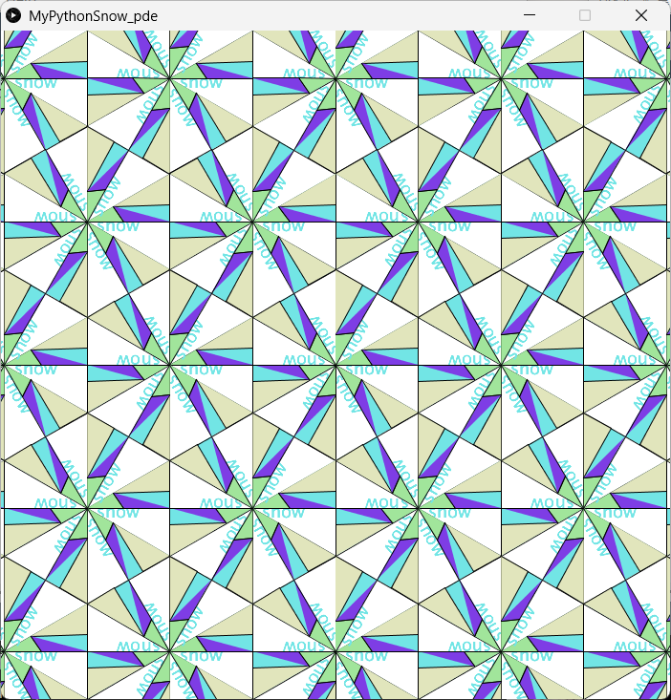
質問:pythonで雪の結晶p6mを実装するにはどうしたらよいでしょうか。
三角形ABCの中に線をかくのは同じですが、少しかえてみましょう。
Aは原点にして、Bの高さを-50にします。y座標の座標系が下がプラスだからです。
ACの間の点をD(dx, 0)、BCの間の点をE(50*a, ey), ABの間の点をF(fx, -fx/a)とします。
辺上の3点とA、B、Cを結んで三角形を作り、色をそめるという方針にします。
画面をクリックするたびに色が変わります。
・setup関数で、dx,ey,fx, col1,col2,col3の初期化します。
・draw関数の3重の平行移動で敷き詰めます。
一番外のfor文での平行移動translateのベクトル(x、y)はx:y=a:3として、
中のfor文で作った基本図形の帯を右上に60度ずらして帯が重ならないようにしています。
中間のfor文での平行移動translateのベクトル(x、y)はx:y1=2a : 0で基本図形の帯を作ります。
一番内側のfor文での平行移動のtranslate(Center, Center) とrotate(r*PI/3)は、描画前に画面中央が
原点(0,0)になるようにして、そのあと、その原点を中心に60度回転をしながら図をかきます。
・基本図形の中身
三角形ABCを水色固定、三角形ADFをcol1のHS(色相彩度)で、
三角形BEFをcol2で、三角形CDFをcol3でかいています。
・三角形ABCをかくときに、[snow]という文字もかいているので、図と一緒に回転したり、平行移動するのがわかります。
座標変換開始pushと座標変換回復popをペアにすること、
多角形の開始beginShapeと終了endShapeをペアにすることがポイントですね。
a = sqrt(3)
ABC = [[0,0],[50*a,-50],[50*a,0]]
dx= 20 #Dx from 10 to 80 Dy=0
ey=-30 #Ey from -5 to -45 Ex=50*a
fx= 40 #Fx from 10 to 80 and Fy = Fx * (-1/a)
col1=0.5
col2=0.7
col3=0.9
def setup():
global dx
global ey
global fx
global col1
global col2
global col3
dx =random(10,80)
ey =random(5,45) * (-1)
fx =random(10,80)
col1 = random(1)
col2 = random(1)
col3 = random(1)
size(700, 700)
textSize(18)
colorMode(HSB, 1) #color by HSB(Hue, Saturation, Brightness)mode
background(0, 0, 1) #Erase canvas
def draw():
global dx
global ey
global fx
global ABC
background(0, 0, 1)
Center = width/2
for j in range(15):
pushMatrix()
translate(50*(j-5)*a , 50*(j-5)*3)
for i in range(10):
pushMatrix()
translate(50*(i-3)*a*2,0)
for r in range(6):
pushMatrix()
translate(Center, Center)
rotate(r*PI/3)
#ABC
fill(0.5, 0.5, 0.9)
beginShape()
for i in range(3):
vertex(ABC[i][0],ABC[i][1])
outvalue= "snow"
text(outvalue, 10, 10) #value
endShape()
#ADF
fill(col1, col1, 0.9)
beginShape()
vertex(ABC[0][0],ABC[0][1])
vertex(dx,0)
vertex(fx,(-1)*fx/a)
endShape()
#BEF
fill(col2, col2, 0.9)
beginShape()
vertex(ABC[1][0],ABC[1][1])
vertex(50*a,ey)
vertex(fx,(-1)*fx/a)
endShape()
#CDF
fill(col3,col3, 0.9)
beginShape()
vertex(ABC[2][0],ABC[2][1])
vertex(dx,0)
vertex(fx,(-1)*fx/a)
endShape()
popMatrix()
popMatrix()
popMatrix()
def mouseClicked():
global dx
global ey
global fx
global col1
global col2
global col3
dx =random(10,80)
ey =random(5,45) * (-1)
fx =random(10,80)
col1 = random(1)
col2 = random(1)
col3 = random(1)
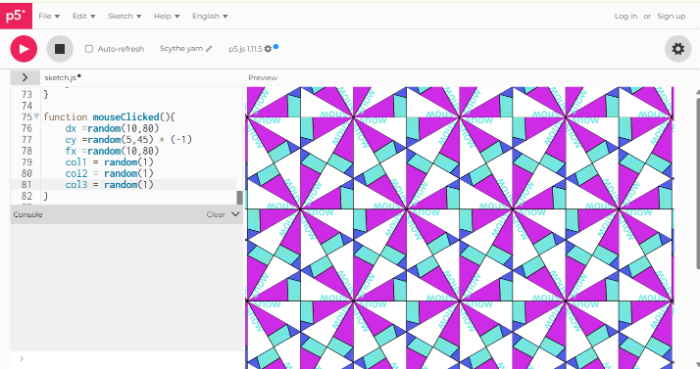
<Javascript>
このコードをp5.jsにしてみよう。
前回はVSの中に拡張機能を導入しましたが、
今回はwebアプリp5.js Web Editorで実行してみよう。
javascriptでは、わかりきったグローバル変数の宣言をしなくてよい分だけ、行数がへります。
本質的には変わってません。
以下を左側のコードの窓にコピーして貼り付けて調整してみよう。
pythonのように字下げでないから、貼り付けはうまくいきやすいでしょう。
前回の注意しましたが、座標変換はpush,popのペアにすること、
setup関数の中で、size関数をcreateCanvas関数に置き換えること。
あとはPythonの記述形式をjavascriptの記述形式に置き換えればOKです。
sqrt(3)にはMath.をつけることくらですかね。
const a = Math.sqrt(3);
let ABC = [[0,0],[50*a,-50],[50*a,0]];
let dx= 20; //Dx from 10 to 80 Dy=0
let ey=-30; //y from -5 to -45 Ex=50*a
let fx= 40; //Fx from 10 to 80 and Fy = Fx * (-1/a)
let col1=0.5;
let col2=0.7;
let col3=0.9;
function setup(){
dx =random(10,80);
ey =random(5,45) * (-1);
fx =random(10,80);
col1 = random(1);
col2 = random(1);
col3 = random(1);
createCanvas(700, 700);
textSize(18);
colorMode(HSB, 1); //color by HSB(Hue, Saturation, Brightness)mode
background(0, 0, 1); //Erase canvas
}
function draw(){
background(0, 0, 1) ;
Center = width/2;
for(let j=0 ; j<15;j++){
push();
translate(50*(j-5)*a , 50*(j-5)*3) ;
for(let i=0; i< 10;i++){
push();
translate(50*(i-3)*a*2,0) ;
for (let r=0; r <6;r++){
push();
translate(Center, Center) ;
rotate(r*PI/3);
//ABC
fill(0.5, 0.5, 0.9);
beginShape();
for(let i=0;i<3;i++){
vertex(ABC[i][0],ABC[i][1]);
outvalue= "snow";
text(outvalue, 10, 10); //value
}
endShape();
//ADF
fill(col1, col1, 0.9);
beginShape();
vertex(ABC[0][0],ABC[0][1]);
vertex(dx,0);
vertex(fx,(-1)*fx/a);
endShape();
//BEF
fill(col2, col2, 0.9);
beginShape();
vertex(ABC[1][0],ABC[1][1]);
vertex(50*a,ey);
vertex(fx,(-1)*fx/a);
endShape();
//CDF
fill(col3,col3, 0.9);
beginShape();
vertex(ABC[2][0],ABC[2][1]);
vertex(dx,0);
vertex(fx,(-1)*fx/a);
endShape();
pop();
}
pop();
}
pop();
}
}
function mouseClicked(){
dx =random(10,80)
ey =random(5,45) * (-1)
fx =random(10,80)
col1 = random(1)
col2 = random(1)
col3 = random(1)
}