Oberfläche einer Kugel - Herleitung der Flächenformel über Projektion auf einen Zylinder
Beschreibe, was du hier dargestellt siehst.
Die Oberfläche einer Kugel mit Radius R wird "Rechtecke" eingeteilt. Beschreibe, was du der folgenden Animation entnehmen kannst. Welche Behauptung kannst du formulieren?
Wie groß ist der Flächeninhalt des Rechtecks? Was kannst du daher über die Oberfläche der Kugel mit Radius R sagen?
Warum ist die Animation kein Beweis für die Oberflächenformel der Kugel? Was muss eigentlich noch gezeigt werden?
Beweis
Hier kannst du nun den Beweis für die Oberflächenformel der Kugel angeleitet durchführen. Im folgenden sind Skizzen aufgeführt und Teile der Kugel und der Zylindermantelfläche dargestellt.
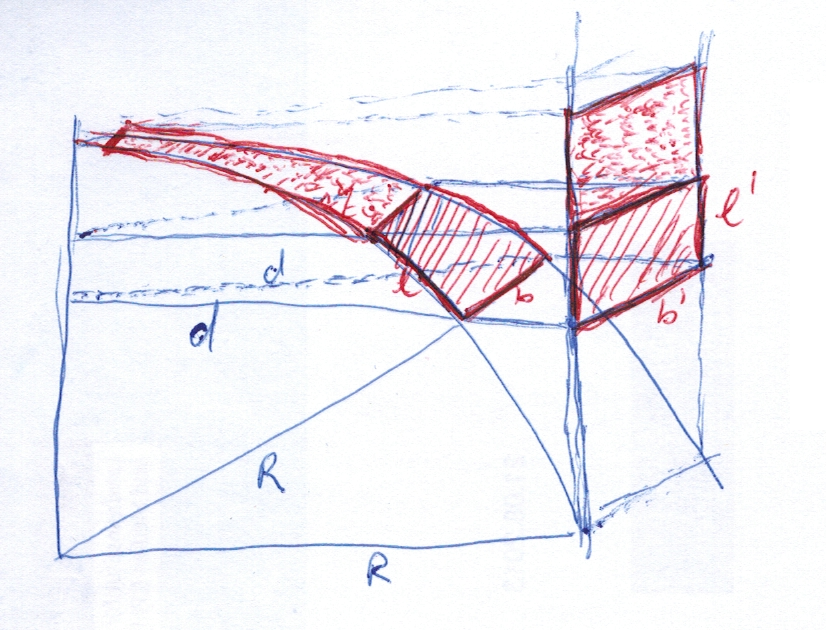
Begründe mithilfe der Skizze, dass die Breite des Rechtecks auf der Zylinderoberfläche proportional zur Breite auf der Kugel ist. Gib den Streckfaktor an.
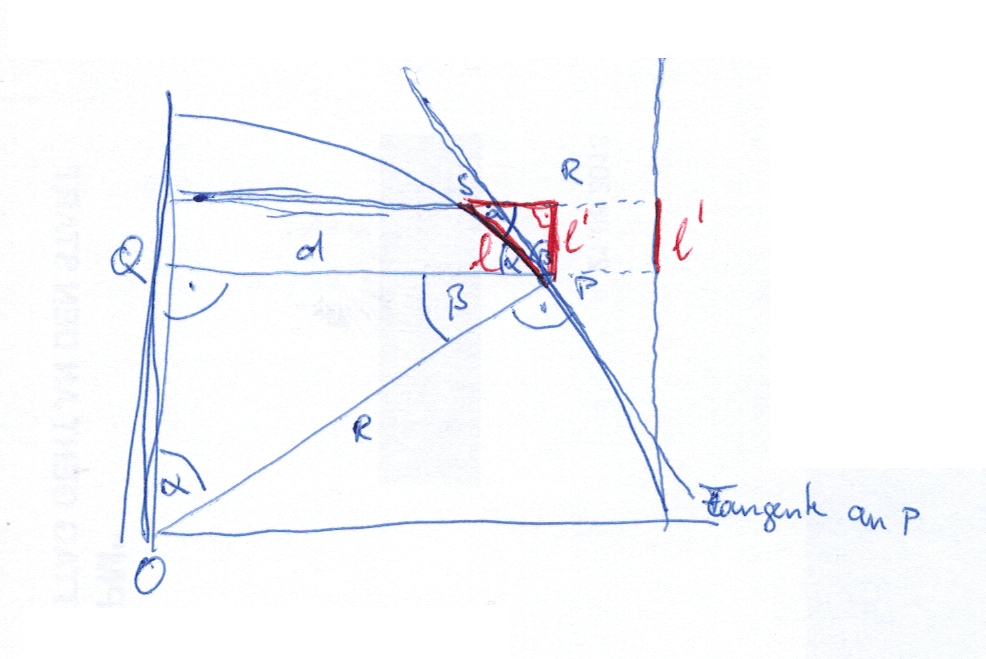
Was kannst du mithilfe der Skizze über die Dreiecke und sagen? Begründe die Winkelbeziehungen. Formuliere eine Verhältnisgleichung für . Löse nach auf.
Berechne die Fläche eines Rechtecks auf der Kugeloberfläche und vergleiche diese mit der Fläche des projizierten Rechtecks auf der Zylindermantelfläche mit Radius . Was stellst du fest?
Begründe hiermit, dass die Oberfläche einer Kugel mit Radius flächengleich zur Mantelfläche eines Zylinders mit der Höhe und dem Radius ist.