Achsenspiegelung an Ursprungsgeraden: Abbildungsmatrix
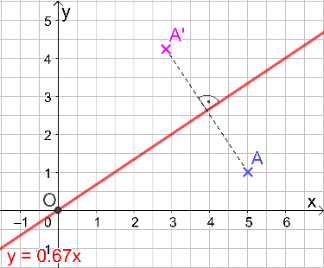
Der Punkt A(x|y) wird durch Achsenspiegelung an der Ursprungsgeraden s auf den Punkt A'(x'|y') abgebildet.
 Die Spiegelachse s bildet mit der positiven x-Achse den Winkel mit dem Maß α.
Ziel: Matrixform der Abbildungsgleichung der Achsenspiegelung an einer Ursprungsgeraden.
Die Zeichnung und die folgenden Schritte helfen dir:
Die Spiegelachse s bildet mit der positiven x-Achse den Winkel mit dem Maß α.
Ziel: Matrixform der Abbildungsgleichung der Achsenspiegelung an einer Ursprungsgeraden.
Die Zeichnung und die folgenden Schritte helfen dir:
- Die Zeichnung zeigt die Abbildung von A auf A'.
- Die Zeichnung ist ergänzt durch 2 rechtwinklige Dreiecke OQA und ORA'.
- Die Katheten der Dreiecke sind entsprechend der Punktkoordinaten beschriftet.
- Die Hypotenusen der Dreiecke sind gleich lang (z LE).
Schritt 1:
Betrachte das Dreieck OQA.
(Bearbeite die Schritte 1 bis 4 in deinem Heft  .)
.)
Schritt 2:
Betrachte das Dreieck ORA'.
Schritt 3:
Die Terme bzw. kommen in den Ergebnissen beider Schritte vor. Setze die Ergebnisse aus Schritt 1 in die Ergebnisse aus Schritt 2 ein. Du erhältst die Abbildungsgleichung in Koordinatenform.
Schritt 4:
Schreibe die Abbildungsgleichung in Matrixform.
Musteraufgabe
Der Punkt A(5|1) wird durch Achsenspiegelung an der Ursprungsgeraden s: auf den Punkt A'(x'|y') abgebildet. Berechne die Koordinaten des Bildpunktes A'. ()