Rezept II
Nach diesem Rezept läßt sich auch online kochen, das entstandene Gericht muss allerdings gespeichert werden, sonst ist die Mühe umsonst!
Nützlicher ist es, das Applet downzuloaden und offline zu kochen.
Die Küchengeräte und Kochutensilien (moebius-werkzeuge etc.) werden mitgeliefert. Das Rezept ist als pdf-Datei erhältlich!
Verzierung mit 6 - Ecken
Diese Seite ist Teil des GeoGebra-Books Moebiusebene (August 2019)
Die Zordnung der Leitkreise zu den Spiegelungen läßt sich mit Hilfe der Scheitelkreise überprüfen: Scheitelkreise sind doppelt-berührende Kreise (DB-Kreise), die Spiegelpunkte des ausgewählten Brennpunkts F liegen auf dem jeweils zugehörigen Leitkreis! Im Applet oben gehört der innere Leitkreis zu , der äußere zu , der mittlere Leitkreis gehört zur Spiegelung am imaginären Kreis, erhält man als Hintereinanderausführung . II.1 : Durch einen beliebigen Punkt P in dem offenen Gebiet zwischen den Kurventeilen, welches die Brennpunkte nicht enthält, gehen zu jeder der 3 Spiegelungen genau 2 DB-Kreise. Für eine 6-Eck-Verzierung muß man aus diesen 3*2 DB-Kurvenscharen je eine auswählen! Wir erklären die Konstruktion der zu gehörenden DB-Kreise: Spiegle P an : P'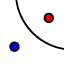 .
.
| Fälle von F aus den Mittellot-Kreis auf P P' (erst P und P', und dann F markieren!) | |
| Die Mittellot-Kreise von P auf F L, bzw. von P auf F L' sind die gesuchten DB-Kreise. | |