RigidPolygon Maker
Points to move/translate RigidPolygon
https://www.reddit.com/r/geogebra
Polygonmaster:
L1,L2,....,L15 select n LL Inputbox RPn
A0-----------A1 ~ 0°
Isometric Grid of Einstein X (aperiodic monotile)
I=Surface(O + u (cos(30°), sin(30°)) + v (cos(-30°), sin(-30°)), u, -10, 10, v, -10, 10)
X={O, I(1, -1), I(1, -1.5), I(2, -2), I(2.5, -3), I(2, -3), I(1.5, -2.5), I(1, -3), I(0, -2.5), I(0, -2), I(-1 / 2, -1.5), I(0, -1), I(-1 / 2, 0)}
α=0..360°
ROT={{cos(α), sin(α)}, {-sin(α), cos(α)}}
J=Surface((ROT (O + u (cos(30°), sin(30°)) + v (cos(-30°), sin(-30°)) - O)) + O, u, -10, 10, v, -10, 10)
Y={O, J(1, -1), J(1, -1.5), J(2, -2), J(2.5, -3), J(2, -3), J(1.5, -2.5), J(1, -3), J(0, -2.5), J(0, -2), J(-1 / 2, -1.5), J(0, -1), J(-1 / 2, 0)}
Aperiodische Parkettierungen (aperiodic monotile - the hat - Einstein)
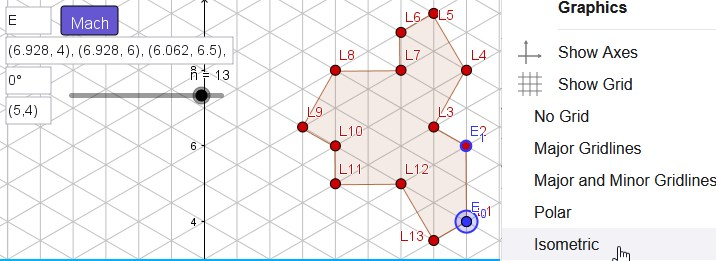
Figure Example M
