[고등수학탐구교실]복소수열의 귀납적 정의
복소수열의 탐구
복소다항식 와 복소수 에 대하여 과 같이 정의된 복소수열 이 있을 때, 의 궤도에 대하여 탐구해보자. (단, , 는 복소수)
앞서 실수열의 변화를 거미줄그림으로 나타내었듯이 복소수열의 변화도 그림으로 나타내면 특징을 한 눈에 알아볼 수 있다. 복소수열의 궤도를 복소평면에 나타내어보고, 그 특징에 대해 탐구해보자.
f(x)=2x인 수열
, 인 수열 이 있다.
일 때, 각 항은 다음과 같다.
, , , , ,
이면, 각 항은 다음과 같다.
, , , , , ,
궤도를 복소평면에 나타내면 그림과 같다.
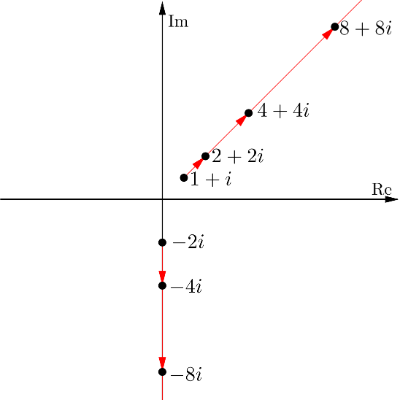
f(x)=x+(2+3i)인 수열
, 인 수열 을 아래 지오지브라 애플릿을 이용하여 첫째항을 하나 정한 후, 궤도를 나타내어보자.
- 입력창에 다음과 같이 입력하면 복소함수 을 만들 수 있다. f(x)=x+2+3i
- 복소수
도구를 선택하여 복소수를 만든 후, 다음항 도구를 이용하여 궤도를 나타내어보자.
- 다음항
도구를 선택한 후, 복소수 z1과 복소함수 f(x)를 선택하면 f(z1)이 만들어진다. 복소수와 복소함수를 선택할 때, 대수창에 있는 대상의 동그라미 옆 부분(노란색 부분)을 선택하면 된다.
도구를 입력하지 않고, 아래와 같이 명령을 이용해도 된다.
다음항(<복소수>,<복소함수>)
예를 들어, 복소수 z1과 복소함수 f(x)가 있을 때, 입력창에 다음과 같이 입력한다.
다음항( z_1 , f )
f(x)=x+(2+3i)인 수열
f(x)=ix인 수열
, 인 수열 을 아래 지오지브라 애플릿을 이용하여 첫째항을 하나 정한 후, 궤도를 나타내어보자.
- 입력창에 다음과 같이 입력하면 복소함수 을 만들 수 있다. f(x)=i x
- 복소수 도구를 선택하여 복소수를 만든 후, 다음항 도구를 이용하여 궤도를 나타내어보자.
f(x)=ix인 수열
f(x)=(1+i)x/2인 수열
, 인 수열 을 아래 지오지브라 애플릿을 이용하여 첫째항을 하나 정한 후, 궤도를 나타내어보자.
- 입력창에 다음과 같이 입력하면 복소함수 을 만들 수 있다. f(x)=(1+i)x/2
- 복소수 도구를 선택하여 복소수를 만든 후, 다음항 도구를 이용하여 궤도를 나타내어보자.
f(x)=(1+i)x/2인 수열
f(x)=(1+i)x인 수열
, 인 수열 을 아래 지오지브라 애플릿을 이용하여 첫째항을 하나 정한 후, 궤도를 나타내어보자.
- 입력창에 다음과 같이 입력하면 복소함수 을 만들 수 있다. f(x)=(1+i)x
- 복소수 도구를 선택하여 복소수를 만든 후, 다음항 도구를 이용하여 궤도를 나타내어보자.
f(x)=(1+i)x인 수열
f(x)=x²인 수열
, 인 수열 을 아래 지오지브라 애플릿을 이용하여 첫째항을 하나 정한 후, 궤도를 나타내어보자.
- 입력창에 다음과 같이 입력하면 복소함수 을 만들 수 있다. f(x)=(x+0i)^2
- 복소수 도구를 선택하여 복소수를 만든 후, 다음항 도구를 이용하여 궤도를 나타내어보자.
f(x)=x²인 수열
지금까지 탐구한 내용을 바탕으로 복소다항식(함수) 와 복소수 에 대하여 과 같이 정의된 복소수열 이 있을 때, 의 궤도에 대하여 설명해보자. (단, 는 실수가 아닌 복소수)
지금까지 탐구한 내용을 바탕으로 복소다항식(함수) 와 복소수 에 대하여 과 같이 정의된 복소수열 이 있을 때, 의 궤도에 대하여 설명해보자.
지금까지 탐구한 내용을 바탕으로 복소다항식(함수) 와 복소수 에 대하여 과 같이 정의된 복소수열 이 있을 때, 의 궤도에 대하여 설명해보자.