Sum of Interior Angles of a Polygon
Introduction
Move triangle vertices A, B. and C. Notice how this changes exterior angle Y and interior angle X.
What is the sum of interior angle X and exterior angle Y?
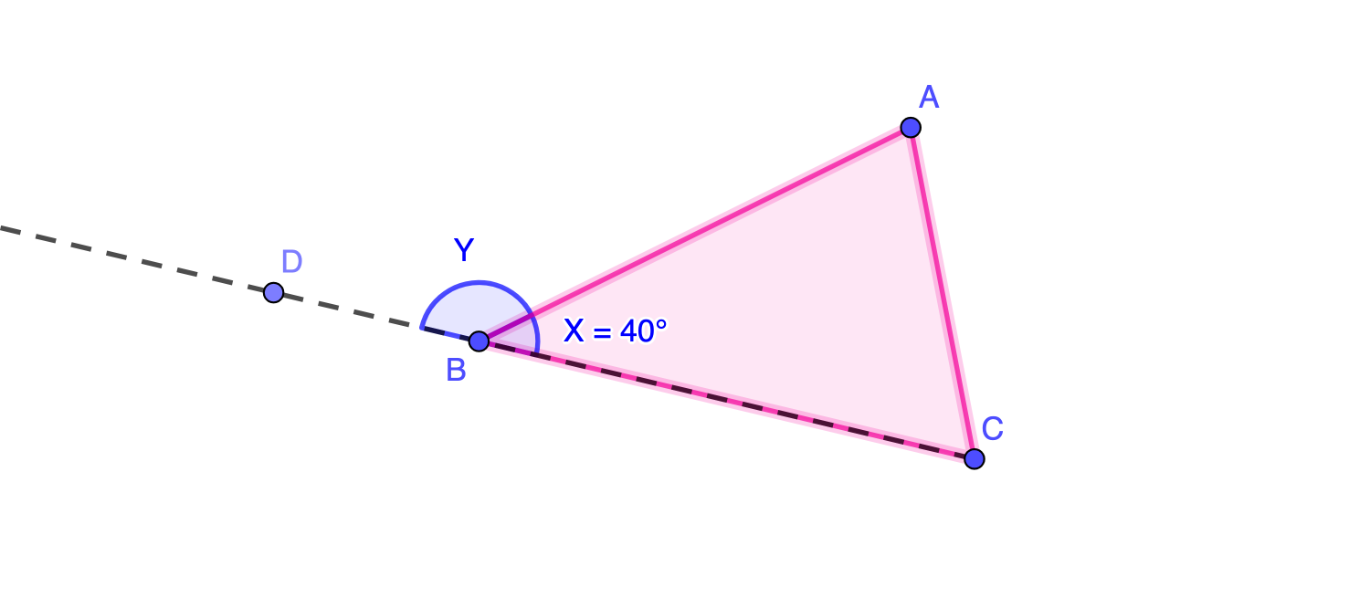
What the value (in degrees) of exterior angle Y?
What is the sum of interior angle U and exterior angle Z?
What is the sum of interior angle W and exterior angle Z?
Now let's take about interior angles only. What is the sum of angles X, U, and W in degrees?
True/False: The sum of the interior angles of a triangle is always 180 degrees.
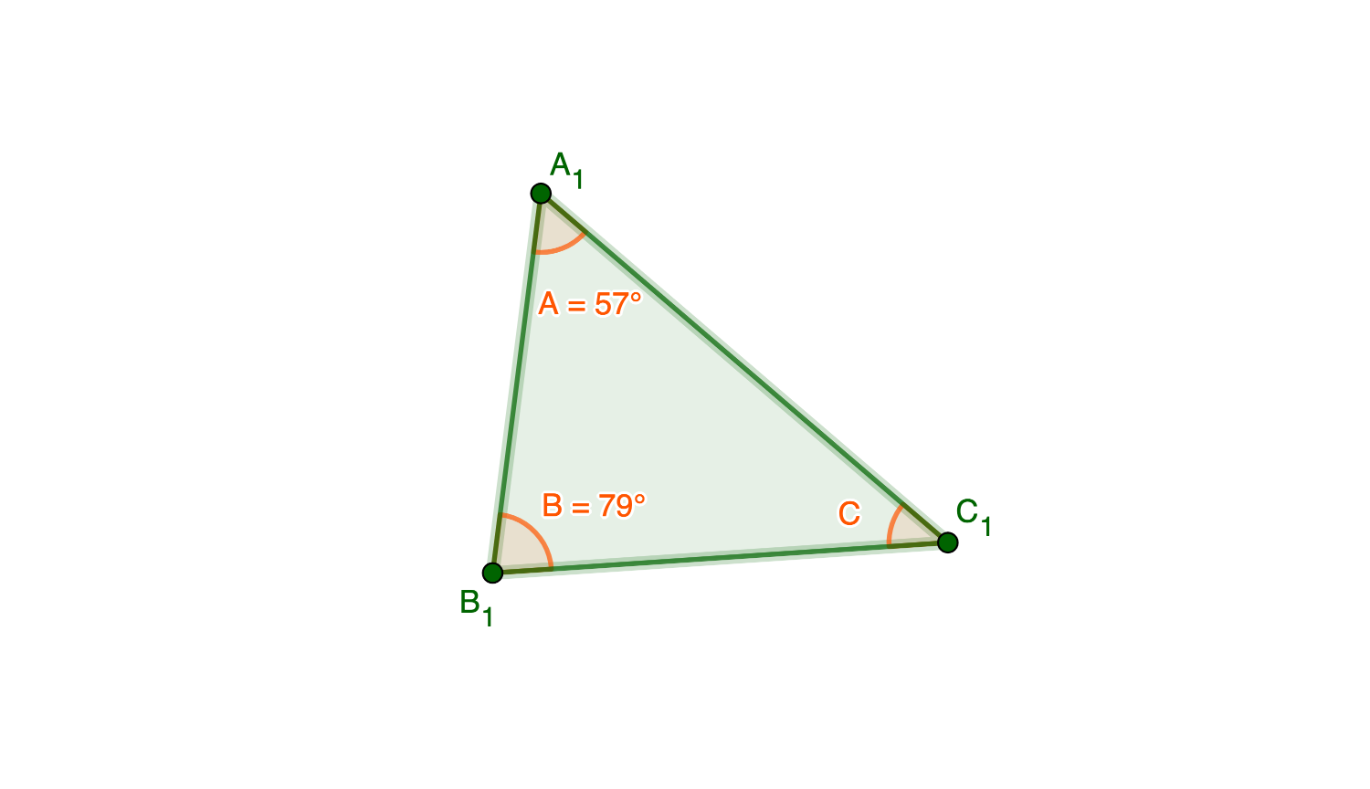
Solve for angle C
Observe this Quadrilateral
How many triangles are in the quadrilateral?
Using your knowledge of interior angles of triangles, what is the sum of the interior angles of the quadrilateral above?
Move the vertices A, B, C, and D around and observe what happens to the degree measurements.
Confirm your answer from above. What is the sum of the interior angles of this quadrilateral?
This is a polygon with FIVE sides. Start at vertex C, use the line segment feature to draw as many triangles as you can that are attached to the other vertices of the polygon.
How many triangles did you create?
Using your knowledge of interior angles of triangles, what is the sum of the interior angles of the polygon above?
Start at vertex B, use the line segment feature to draw as many triangles as you can that are attached to the other vertices of the polygon.
How many sides does this polygon have?
How many triangles were you able to create?
Using your knowledge of interior angles of triangles, what is the sum of the interior angles of this polygon?
How did you use the number of triangles to find your answer? Provide an equation.
Start at vertex F, use the line segment feature to draw as many triangles as you can that are attached to the other vertices of the polygon.
How many sides does this polygon have?
How many triangles were you able to create?
Do you notice a relationship between the number of sides of the polygons and the number of sides you were able to create? Attempt to create an equation to represent the relationship using this polygon.
Using your knowledge of interior angles of triangles, what is the sum of the interior angles of this polygon?
If you have a triangle with n number of sides, how would you represent the number of triangles you can create in that polygon?
Using all of the information we have collected so far about the sum of interior angles, can you create an expression that represents the sum of the interior angles for a polygon with n number of sides? If so, provide it.
