Exploration des Beugungsintegrals
Kontinuierliche Fallsummierung einzelner Wellen: Mit dem vorliegenden Applet ist es möglich, das Integral der Beugung hinter einem Spalt, das auf der Grundlage des Huygens-Fresnel-Prinzips geschrieben wurde, zu untersuchen und es mit der Fresnel-Näherung zu vergleichen. Dieses Integral, aufgeteilt in seinen realen und imaginären Teil, führt zu verallgemeinerten Fresnel-Integralen (nennen sie hier so), die den gewöhnlichen Fresnel-Integralen ähneln.
Applets zur diskreten Summierung einzelner Wellen: -Simulationsprogramme zum Thema: Intensität vieler interferierender Punktquellen wurde bereits früher betrachtet. Beginnen Sie mit dem Applet.
**************************************************************************************************************************************
Der Spalt der Breite b wird von links mit einer ebenen, monochromatischen Lichtwelle der Wellenlänge λ beleuchtet, die sich in x-Richtung ausbreitet. Am Spalt sind die Phase und die Amplitude der ebenen Welle konstant. Wir bezeichnen die Amplitude der Welle am Spalt als . Die Amplitude der Welle pro Element der Spalt der Breite dy ist offensichtlich: .
Nach dem Fresnel-Huygenssches Prinzip kann jeder infinitesimal kleines Element dy des Spalts als Emittent einer Kugelwelle in einem Beobachtungspunkt P(L,yo) angesehen werden, die sich schreiben lässt als komplexe Amplitude:
mit
r -Abstand vom Zentrum der Kugelwelle (mit y-Koordinate) zum Beobachtungspunkt, ω=2πν-Kreisfrequenz, k=2π/λ-Wellenzahl, t-Zeit,
-das Gesetz, durch welches die Amplitude der Schwingungen mit dem Abstand nimmt ab. s-Grad dieser Abnahme. Beugung am eindimensionalen Spalt (wie sich herausstellt) hat das Gesetz der Amplitudendämpfung den Grad s = 0,5.
So, haben wir am Beobachtungspunkt folgende Summe von Schwingungen einer Richtung von allen Teilen des Spaltes die komplexe Feldamplitude:
; c ist ein Proportionalitätsfaktor.
Mit Hilfe von Vereinfachungen erhält man bekannte: Fresnel und Fraunhofer-Näherungen. Numerische Berechnungen des Beugungsintegrals ermöglicht die Beugungsregionen (Nahfeld, Übergangsfeld und Fernfeld) näher zu untersuchen, die sich oft wesentlich von den Ergebnissen dieser Näherungen unterscheiden.

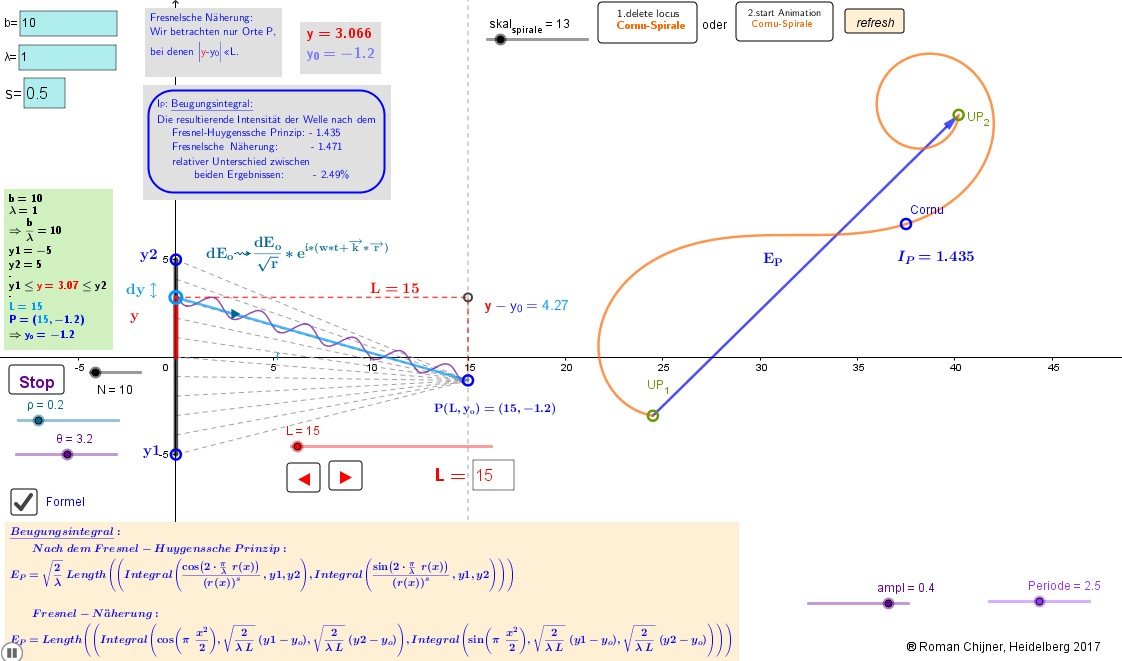
Ansicht des Applets: