シェルピンスキーのギャスケット
このワークシートはMath by Codeの一部です。
アート、背景と関連、実装、バリエーションの順に見ていきましょう。
重いアプレットが多数のっているので、開くまでに停止に近い動作になることがあります。
環境によっては、負担の大きいシートになっていることをご承知おきください。すみません。
<シェルピンスキーのギャスケット>
白い正三角形を相似な三角形4つに分割して、中央の1つに着色します。
残りの3つの白い正三角形に対しても同じ操作をします。
これを繰り返した図形がシェルピンスキーのギャスケット(詰め物、シール材)
シェルピンスキーのギャスケット
1.背景と関連
シェルピンスキーのギャスケット(Sierpinski gasket)は、フラクタル[fractal]図形(自己相似形)
といわれるものの1つです。
たとえば、シダの葉を拡大すると、そこに全体と相似な図形が見えてきます。
地形では、リアス式海岸などもそれに近いです。ギザギザした地形を拡大した地図にまた、
細かいギザギザした地形が見えてきます。
体では小腸の柔突起がそれに近いです。
いぼの凸凹を拡大するとさらに同じような凸凹が見られます。
自己相似形は、全体と部分が相似形で、拡大を繰り返しても全体と同型のものが見られる。
数学が先か?自然が先か?
人間が先か?神が先か?
フランクタル図形自体は人工物ですが、
自然界にも通じる無限性を感じさせる不思議さを漂わせていますね。
シェルピンスキーのギャスケットに関係するのは「フラクタル」だけではありません。
「パスカルの三角形」の偶数を●、奇数〇をとかくと〇●で塗りわけられたギャスケットが浮かびます。
数を分類すると模様ができる、つまり「剰余類模様」です。
また、パスカルの三角形を●と〇に直すのではなく、上に〇をかいて、次も〇,〇にします。
次は両端は〇にして、間は上の2つ両方が〇のときだけ●で、それ以外は〇というルールで、隣接するセルを色分けします。
こんな風に、隣接の状態から次々と生成される模様を「セルオートマトン」といいます。
<フラクタル>
フラクタル図形には、いろいろあります。
フラクタルな平面図形には、
コッホ曲線、
シェルピンスキーのカーペット、
ドラゴンカーブ、
ヒルベルト曲線、
。。。。。。などなど。
興味のある人は、ネットやAIで調べてみよう。
しかし、フラクタルは平面図形だけではありません。
3次元でもあります。
それがメンガーのスポンジです。
これは、立方体を3分の1の大きさの相似形27個の分割して3方向から中央にあるものを合計7個取り去る。残った20個の立方体についても同じことをする。これを繰り返します。
メンガーのスポンジ
道順数の和
<パスカルの三角形>
パスカルの三角形は、(最初の段に1をかき、その下に)
1と1を並べます。
その次の段からは、両端が1で、間は真上の数の和をかきます。
だから、
(1段目は1)
2段目は1,1
3段目は1,2,1
4段目は1,3,3,1
5段目は1,4,6,4,1、
。。。。。。
のようになります。
ルールはいたって単純ですが、
そこにはいろんな秘密が隠されています。
段ごとにみると、5段目は(1,4,6,4,1)=(4C0,4C1,4C2,4C3,4C4)に対応しています。
これって、組み合わせの記号を使うとすごそうな雰囲気を醸し出してますが、
パチンコの玉が上からその場所にたどり着く道順として考えれば、
当然の結果です。
玉が左右に流れ落ちるのだから、
左はしや右はしでもない限りは、途中で反対に何回かそれる。
頂上から任意の点への道順数は、道順数の和の法則を使えば、
組み合わせnCr(n個からr個選ぶ組み合わせ数)で表せるのです。
(例)
上の図のように、頂上から5段目の中央につくには、頂点から左2回と右2回を適当な順番で落下します。
2+2=4回進むうちに、右向きを2回選ばないといけません。
だから、5段目の中央が6=4C2(4つから2つ選ぶ組み合わせ数)になるね。
たし算を繰り返すだけで、組み合わせ4C2が計算できてしまうこともわかる。
だから、パスカルの三角形を作ると、組み合わせの公式を覚えたてのときの確認にも使えるね。
パスカルの三角形にはおもしろい性質がいろいろ隠れているようです。
それは、中学入試や大学入試の材料としてよく取り上げられてきました。
たとえば、
・段ごとの数の和は2のべき乗になる。
段ごとの和は1段1、2段2、3段4、4段8、……のようにn段目は2の(n-1)乗になっている。
・だから、N+1段目の和は「nC0+nC1+.....+nCn-1+nCn=2のn乗」という等式が成り立つ。
・頂点から右下がりに数列をみると、
1列目が1の連続列、2列目が自然数、3列目が三角数、4列目が三角すい数、……。
パスカルの三角形
パスカル三角形の中の数列群
<剰余類模様>
パスカルの三角形を偶数と奇数で色分けすると、きれいな模様ができた。
このように数を割り算の余りで分類すると綺麗な模様が見えるは、
なにもパスカルの三角形に限ったことではないね。
たとえば、
アイゼンシュタイン整数というのがある。
x3=1の1つの解ω=(-1+i √3)/2を整数環Zに添付した環Z[ω]だ。
Z[ω]は a+bω( Z∍a,b )の形にかける。この複素数の集合の要素をnとしよう。
nをガウス平面にかくと、原点と中心にした正三角形状の格子点となる。
たとえば、3を法とする剰余系を作ったときのことを思い出そう。
3の倍数の集合3Zは、3とZの要素nをかけた3nの集合だった。
3n,3n+1,3n+2が剰余系Z3={[0],[1],[2]}に対応したね。
同様に考えて、3のかわりにzp = 1- ωとする。
これにn= a+bωをかけて、
zp*n、zp*n-1, zp*n+1の3つの集合をつくろう。
そうすると、格子点が3色に塗り分けられるね。
つまり、
アイゼンシュタイン整数Z[ω]はB=(1-ω)を法としてB-1,B,B+1の3種類に色分けできる。
a+bωを(1-ω)で3色に塗り分けよう。
<セルオートマトン>
セルが並んでいるときに、隣接するセルの状態から状態が決まっていくのがセルオートマトン。
上から1段目、2段目、……の数値を1世代、2世代、……と呼ぶことにするとき、
各世代は1方向に並んでいます。これを1次元といいます。
値が0,1の2つとしたとき参照する要素がパスカルの三角形のように2つのときは、
次の世代は22=4パターンがありましたが、mod 2の剰余という1つの式にすることができます。
参照する要素数を変えたり、法をmod3に変えたりしたら、ちがう模様が作れるでしょう。
セルオートマトンという言葉は知識として要求はされませんが、
中学入試でも、0,1が隣接して生成されるルールから規則性を予測する問題がたまに出題されます。
だから、セルオートマトンは、名前はいかめしいかもしれません。
ただ、中身は、「フィボナッチ数列のようにたし算するだけで、値が決まり、
その値を剰余分類することで固定した値の集合のどれかになるというものだ」
と考えれば、小学生でもわかるような内容だと言えるかもしれませんよ。
セルオートマトンの法を変える
2.実装
シェルピンスキーのギャスケットよりも
パスカルの三角形の方が、汎用性があるので、
先に取り組み、そのあとでギャスケットにとりくみましょう。
まずは、geogebraです。
<geogebara>
質問:geogebraでパスカルの三角形をつくるにはどうしたらよいですか。
パスカルの三角形は長方形をつみあげて、中に数を上から規則正しく入れた形になります。
普通に長方形をくっつけていくと、長方形だらけ、辺だらけ、点だらけになります。
geogebraの「数式」はオブジェクトの数だけ行を消費するのですごいことになってしまうでしょう。
それは嫌なので、平行移動のtranslateと要素列のsequenceのうまく組み合わせてみましょう。
原点から、x軸の正負の方向に1はなれた2点を頂点とし、
原点から、y軸の正方向に1はなれた1点を通るたて1、よこ2の長方形を作ります。
長方形st=Polygon((-1,0),(1,0),(1,1),(-1,1))です。
長方形をスライドするための2つのベクトルを用意します。
H=(2,0),R=(-1,-1)
Hは右に2だけ動くベクトルで、stのよこの長さはちょうど2です。
たとえば、Translate(st,Vector(H 1),Translate(st,Vector(H 2)
は長方形stをH1回移動、H2回移動 した2つの長方形です。stの右わきに2個かぶらずに並びます。
もし、H方向に1,2,3移動して3つ長方形を作りたかったらSequenceの出番です。
S(3)=Sequence(Translate(st,Vector(H i)),i,1,3)
これだけで、stの右わきに3個かぶらすに並びます。
S(j)=Sequence(Translate(st,Vector(H i)),i,1,j)
これだけで、stの右わきにj個だけ列車のように並びますね。
しかし、パスカルの三角形は1段目は1個、2段目は2個、3段目は3個必要です。
だから、段目によって長方形の個数がちがうし、
段が進むごとに、1個目の長方形を1つ下に、1つ左にずらして作ります。
j段目に作る長方形たちはS(j)と考えると、1個目が1つ下に、1つ左にずれるので重なりません。
つまり、Sequece(Translate(S(j), Vector(R j), j, 0, cj)
とすると、jは0段目からCj段目まで列車がたてにつながります。
S(j)の中身を直接かくと、次のようになります。
l1=Sequence(Translate(Sequence(Translate(st,Vector(H i)),i,1,j),Vector(R j)),j,0,cj)
こうすると、長方形がパスカルの三角形の形に上から順に並びます。
次は長方形の中にかく数字です。
とりあえず確認しやすくするために、i列j段目にはi+j-1という数字が入るように作ってみます。
ただし、文字はtext(文字,x座標,y座標)として指定します。だから、長方形のtranslateは使えません。
j=0とすると、iが1増えるたびに文字のx座標を2ずつ増やす。iが1なら2です。
これからx座標は2*i, y座標は0にします。
次にj=1とすると、1個目の文字を1つ下に、1つ左にずらします。
だから、x座標は2*i -j , y座標は-jにします。
実際は、文字の大きさもあるので、横に-0.7ずらし、たてに+0.2ずらします。
だから、Sequence(Sequence(Text(i+j-1,(2 i-j-0.7,-j+0.2)),i,1,j),j,1,cj)
これで、動きを確認したら、i列j段目には(j-1)C(i-1)を入れる必要がありますね。
組み合わせ計算の関数はCASにはありますが、数式に連動して使うのが難しいので、ツールで作ります。
「数式」にn=20, r=5と入れます。
sequence(n)と入力して、もしl4にされたら、l4=Sequence(n)となります。
Product(l4)と入力して、もしaにされたら、a=Product(a)になります。
ここで、geogebraのメインメニューの下の方のツールの「ツールの新規作成」を選びます。
入力としてnを選び、出力としてaを選び、ツールの名前をfactにしましょう。
これで、階乗関数fact(n)を定義したことになります。
次にfact(n) /fact(n-r) fact(r) と入力して、b= と 表示されたら、またツール化します。
ツールの「ツールの新規作成」を選びます。
入力としてn、rを選び、出力として、bを選び、ツールの名前をnCrにしましょう。
これで、コンビネーションが関数としてnCr(n,r)と入れて使えます。
Text(i+j-1, のところをText(nCr(j-1, i-1), に変更すれば、これで、パスカルの三角形の数になります。
Sequence(Sequence(Text(nCr(j-1, i-1),(2 i-j-0.7,-j+0.2)),i,1,j),j,1,cj)
この1行を「数式」に入力すればよいです。
セルオートマトンのように、剰余だけの模様にしたければ、
P=nCr(j-1, i-1)とおいたとき、
if(Mod(P, 2)==0, "●","")とすると、偶数なら●、奇数なら非表示にできます。
If(Mod(nCr(j-1, i-1),3)≟0,"●",If(Mod(nCr(j-1,i-1),3)==1,"◎",""))とすると、
3の倍数なら●、1余るなら◎、それ以外は非表示にできます。印はなんでもいいです。
質問:geogebraでシェルピンスキーのギャスケットを作るにはどうしたらよいでしょうか。
パスカルの三角形を作るのと似た発想をします。
オブジェクトを大量に作るのではなく、基本となる図形を縮小コピーした図形列を作るのです。
Sequence、Dilate、Elementの3つを連携して使います。
まずは、基本になる全体の正三角形ABCを作ります。
そして、3辺の中点D,E,Fをとりましょう。
H={A,B,C}と頂点リストHを作ります。
底辺がABでABの中点がFです。
右辺がBCでBCの中点がDです。
左辺がACでACの中点がEです。
Dilate( <オブジェクト>, <拡大率>, <拡大の中心点> )が縮小図形の作り方です。
Dilate(D,(1/2),Element(H,1)),
Dilate(E,(1/2),Element(H,1)),
Dilate(F,(1/2),Element(H,1))
これで、3点DEFがHの1番点Aを中心に1/2サイズで引き寄せられました。
これをPolygon()でくるむと、三角形DEFを点Aよりにした縮図三角形のできあがりです。
つまり、
S1=Sequence(Polygon(
Dilate(D,(1/2),Element(H,k)),Dilate(E,(1/2),Element(H,k)),Dilate(F,(1/2),Element(H,k))),k,1,3)
のS1というのは、三角形DEFの縮図をA,B,Cよりに3つ作った図列なのですね。
S1は第1世代で3個です。
S2=Sequence(Dilate(S1,(1/2),Element(H,k)),k,1,3)
これは、S1の3個をA,B,Cに引き寄せた、第2世代の3*3=9個の図列です。
S3=Sequence(Dilate(S2,(1/2),Element(H,k)),k,1,5)
これは、S2の9個をA,B,Cに引き寄せた、第3世代の9*3=27個の図列です。
S4=Sequence(Dilate(S3,(1/2),Element(H,k)),k,1,5)は第4世代の81個。
S5=Sequence(Dilate(S4,(1/2),Element(H,k)),k,1,5)は第5世代の243個。
S6=Sequence(Dilate(S5,(1/2),Element(H,k)),k,1,3)は第6世代の729個。
3。バリエーション1
<Geogebra>
質問:シェルピンスキーのギャスケットは正三角形でできていた。正方形にしたシェルピンスキーのカーペットを作るにはどうしたらよいですか。
基本となるのは正方形ABCDの中心Eに1/3に縮小した正方形p0です。
これを1/3に縮小しますが、縮小の中心は、正方形の4頂点A,B,C,Dと辺の中点F,G,H,Iです。
この8点をリストPsにして、
p1=Sequence(dilate(p0,1/3,Ps(k)), k, 1, 8)としましょう。
p1に対して同じことをした結果をp2にします。
p2=Sequence(dilate(p1,1/3,Ps(k)), k, 1, 8)
p3=Sequence(dilate(p2,1/3,Ps(k)), k, 1, 8)
p4=Sequence(dilate(p3,1/3,Ps(k)), k, 1, 8)
スライダーnを1から4として、
p1,p2,p3,p4の表示条件をそれぞれ、n>=1, n>=2, n>=3,n>=4設定して、
スラーダーnをアニメーションOnにすれば、カーペットのレベルが変化しますね。
シェルピンスキーのカーペット
4.バリエーション2
<Processing>
Processingというアート系の環境がある。
この環境では、言語が選択できる。
基本はjavaだけれど、pythonが使えるようになっている。
このprocessingのデザインがjavascriptに移植されたモジュールp5.jsがある。
ということで、今回は、言語というよりも
「アート開発の環境・デザインとしてのProcessing」に触れてみよう。
processingの基本は3要素です。
グローバル変数宣言、
画面サイズなどのsetup関数、
描画を繰り返すdraw関数です。
ふつうは、この順にかいていきます。
グローバル変数宣言
void setup() {
画面たて横さいずの指定など
}
void draw() {
繰り返し描画の本体
}
<java in Processing>
javaなどの静的に型チェックの入る言語では、
型宣言をint, float, longのように、最初に使うときはつけるので、ルールに従いましょう。
まず、geogebraの宣言的リスト記法は使えませんから、for文の大活躍になります。
宣言的リスト記法が使えたとしても、モジュールをいろいろimportしたりすることになるでしょう。
なれるために、モジュールなしで素のjavaでやります。
長方形stのたてが1、よこが2で、それをH=(2,0)ベクトルでTranslateした図形列は
geogebraなら、S(j)=Sequence(Translate(st,Vector(H i)),i,1,j)と一行でかけました。
javaでは、
for (int i = 0; i < j+1; i++) {
pushMatrix();//座標変換開始
translate(i * 20 +Center, 0);
rect(20, 20, 20, 10)
}
popMatrix();//座標変換復元
となります。
また、相対座標ではないので、1個目の位置を横はばの半分Center=width/2にする必要があります。
l1=Sequence(Translate(Sequence(Translate(st,Vector(H i)),i,1,j),Vector(R j)),j,0,cj)
宣言的リスト記法を入れ子にすると、for 文も入れ子になります。
このように、冗長で古風な記法になりますが、
行処理をあとd、行の更新がすることができます。
nextline[i] = (line[i + 1] + line[i]) % mod;
これで、次の行のセルのi番目の値が、i番目とi+1番目の和をmodで割った剰余に設定できています。
これで、geogebraのアプリのように組み合わせの計算に頼ることがなくなっています。
すばらしい。
さらに、
mouseClicked() ,mousePressed()
などによって、セルオートマトンの剰余系での法modの変更が簡単にできます。
その新しい法でのパスカルの三角形をパッとかいてくれるものが作れます。
javaの配列が固定長なので、pythonのような柔軟さがなく、コードが冗長になりますが、
色をHBにしてH色相(色を虹のように波長でならべたときの位置)、S彩度(あざやかさ)をmodに応じた剰余のmodに対する割合にすることで、
とても鮮やかに変化します。
B明度(あかるさ)は0.9くらいがよいでしょう。
processingをインストールして、
下にあるコードを貼り付けて実行すると、アプリが表示されます。
クリックするたびに模様と色が変化しますよ。
geogebraの画面での1の大きさをsize=10として、長さの単位にしています。
このsizeを小さくすると、表示される長方形も小さくなります。
いろいろ修正してみてください。
[IN]MyPascal.pde
//==================================================
int mod = 2;
void setup() {
size(1400, 700);
colorMode(HSB, 1); //color by HSB(Hue, Saturation, Brightness)mode
background(0, 0, 1); //Erase canvas
noStroke(); //no Edge
}
//H=(20,0),R=(-10, 10) Vector for translateing to rect
void draw() {
int[] line = {1};
background(0, 0, 1); //Erase canvas
int cj =64; // count of lines
int size = 10; // canvas unit for 1
float wd = size * 2-1; //rect width
float ht = size-1; //rect heigh
float Center = (float)width/2; //Top x-position
for (int j = 0; j < cj; j++){
pushMatrix();
//start triangles_drawing
translate(-j * size, j * size); // tlanslate(rect, R j)
for (int i = 0; i < j+1; i++) {
pushMatrix();
//start line_drawing
translate(i * size*2 +Center, 0); // tranxlate( rect, H i)
float HSBvalue = line[i]*1.0/mod;
int value= line[i];
fill(HSBvalue, HSBvalue, 0.9);
if(value>0){
//text(String.valueOf(value), wd, ht); //value
rect(size*2, size*2, wd, ht); //rect
}
//line drawing complete!
popMatrix();
}
// lineUpdating
// adding zero to both side of line for cell_calculation
int[] BOUNDARY = {0};
line = splice(line, BOUNDARY, 0);
line = splice(line, BOUNDARY, line.length);
//cell_calculation by modulo
int[] nextline = new int[line.length + 1];
for (int i = 0; i < line.length - 1; i++){
nextline[i] = (line[i + 1] + line[i]) % mod;
}
line = nextline;
//trianlges drawing complete!
popMatrix();
}
}
void mousePressed(){
mod = int(random(2, 30));
}

<Python in Processing>
質問:上のプログラムをpythonに移植するにはどうしたらよいでしょうか。
・javaをPythonに直すには、かなり形式的・機械的にできる部分が多いです。
変数の型をとり、文末の「;」をとります。また、関数のはじまりをreturnがない場合のvoidから、
defにしましょう。関数やfor文での改行には「:」をつけます。
また、文のかたまりである{ }のくくりをなくして、字下げ(インデント)の数でくくりを表示します。
コメントの先頭は//から#にしましょう。
・形式以外で重要なのは、グルーバル変数です。
Pythonでは、先頭で宣言するだけでは、グローバル変数になりません。使いたい関数の中の先頭で
global 変数名
とかくことで、初めてグローバル変数として使うことができます。
・同じくらい重要なのは、配列の操作です。
javaでは、固定長が基本なので、arrayクラスなどのモジュールを導入しないと可変に使えませんが、pythonでは自由にリストの最初と最後に0をつけたりできます。
0だけつかって初期化するには nextline = [0]*newSizeというかきかたができます。
ただの移植ではつまらないので、cjをグローバル変数にして、クリックしたときに適当に変わるようにしました。そうすると、単位となるサイズが固定だとおかしなことになるので、
size = 700/cj
という式で、画面サイズに合わせてセルサイズが変わるようにしてあります。
また、ちょっと横が長すぎるので、画面サイズも、セルサイズもたての2倍から、1.4倍くらいにすることで、正三角形に近くしtみました。もっときれいに見せたい人は、
この数値関係を研究して、修正してみてください。
[IN]MyPythonPascal.pde
#==================================================
cj = 64
mod = 2
def setup():
size(1000, 700)
colorMode(HSB, 1) #color by HSB(Hue, Saturation, Brightness)mode
background(0, 0, 1) #Erase canvas
noStroke() #no Edge
def draw():
global mod
global cj
line = [1]
background(0, 0, 1)
size = 700/cj
wd = size * 1.4-1
ht = size-1
Center = width/2
for j in range(cj):
pushMatrix()
translate(-j*0.7 * size, j * size)
for i in range(j+1):
pushMatrix()
translate(i * size*1.4 +Center, 0)
HSBvalue = line[i]*1.0/mod
value= line[i]
fill(HSBvalue, HSBvalue, 0.9)
if value>0:
#text(str(value), wd, ht) #value
rect(size, size, wd, ht) #rect
popMatrix()
line.append(0)
line.insert(0,0)
newSize = len(line)+1
nextline = [0]*newSize
for i in range(newSize-2):
nextline[i] = (line[i + 1] + line[i]) % mod
line = nextline
popMatrix()
def mouseClicked():
global mod
global cj
mod = int(random(2, 30))
cj = int(random(30, 300))
print("cj={},mod={}",cj,mod)
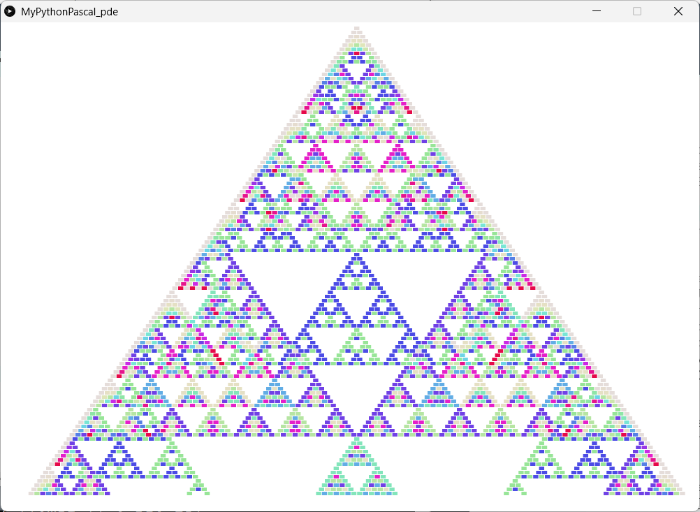
<JavaScript in VScode with p5.js>
VScodeの環境があれば、processingをインストールしなくてもwebで表示できます。
ブラウザですから、2本指で拡大縮小などもできます。
VScodeの拡張機能の「p5.vscode」インストールします。
手動ではなく、メインメニューの「表示」の「コマンドパレット」を選び、
「Create p5.js Project」とタイプして、空のフォルダなどを指定しましょう。
すると、そこがp5.js用のプロジェクト一式が用意されます。
ライブラリ、jsonファイル,cssファイル,htmlファイル.jsファイルができます。
そのjsファイルは、名前がSketch.jsとなっています。
ここに、javaScriptでprocessing的なコードを書いていきます。
(詳しくは、https://p5js.org/tutorials/setting-up-your-environment/)を参照してください。
コードを実行させるに プルジェクトにあるindex.htmlを右クリックして「 Open Live Server」
を選びましょう。
(ダグルクリックしてしまうと、ただ、index.htmlが編集用に開いてしまうだけです。 また、index.htmlをファイルエクスプローラから開いても、うまく動きません。プロジェクトと環境と込みで動くようになっているのですね。)
javascript は見かけ上、pythonよりもjavaに似ているので、それを移植しましょう。
3つほど注意点があります。
・形式的な移植は、変数の型int, floatの宣言部分はletにします。
割り算の結果をfloatにしているところは(float)をとってしまいます。
・setup()関数の先頭にかく画面サイズがsize(, )ではなく、createCanvas(,)になっています。
pushMatrixがpushに、posMatrixがpopに短縮されています。
・配列の宣言はサイズではなく、pythonのリストのように空のまま let nextline = [];
のように宣言して、そのつど、nextline.push(中身);として、追加式にします。
大きめに表示されて、はみ出してしまうことがあるので、段数cjを32にして小さくしています。
出来上がったら、ファイルエクスプローラー
[IN]sketch.js
#=============================================
//グルーバル変数
let mod = 2;
function setup(){
createCanvas(1400, 700); //NG size(1400,700);
colorMode(HSB, 1); //color by HSB(Hue, Saturation, Brightness)mode
background(0, 0, 1); //Erase canvas
noStroke(); //no Edge
}
//H=(20,0),R=(-10, 10) Vector for translateing to rect
function draw() {
let line = [1];
background(0, 0, 1); //Erase canvas
let cj =32; // More smaller
let size = 10; // canvas unit for 1
let wd = size * 2-1; //rect width
let ht = size-1; //rect heigh
let Center = width/2; //Top x-position
for (let j = 0; j < cj; j++){
push(); //NG pushMatrix();
//start triangles_drawing
translate(-j * size, j * size); // tlanslate(rect, R j)
for (let i = 0; i < j+1; i++) {
push(); //NG pushMatrix();
//start line_drawing
translate(i * size*2 +Center, 0); // tranxlate( rect, H i)
let HSBvalue = line[i]*1.0/mod;
let value= line[i];
fill(HSBvalue, HSBvalue, 0.9);
if(value>0){
//text(String.valueOf(value), wd, ht); //value
rect(size*2, size*2, wd, ht); //rect
}
//line drawing complete!
pop(); //NG popMatrix();
}
// lineUpdating
// adding zero to both side of line for cell_calculation
let BOUNDARY = [0];
line = splice(line, BOUNDARY, 0);
line = splice(line, BOUNDARY, line.length);
//cell_calculation by modulo
let nextline = [];
for (let i = 0; i < line.length - 1; i++){
nextline.push ( (line[i + 1] + line[i]) % mod ) ;
}
line = nextline;
//trianlges drawing complete!
pop(); //NG popMatrix();
}
}
function mousePressed(){
mod = int(random(2, 30));
}