This activity belongs to the GeoGebra book Voronoi Paintings.
The precise adjustment of the Voronoi diagram to the silhouettes of the positive space observed in the two previous paintings invites us to ask the following question: To what extent does the Voronoi diagram of a painting provide information about the silhouettes of its positive space? To attempt to answer this question, let's go back to the case of point sites.
It is clear that for each collection of sites, its Voronoi diagram is unique. However, the converse does not necessarily have to be true. In other words, given a plane division into n Voronoi regions, there may be more than one set of n sites that generates it.
For example, let's consider four sites arranged at the vertices of a rectangle. Their Voronoi diagram is very simple: the pair of medians that bisect the pairs of opposite sides of the rectangle. However, the set of four sites placed at the vertices of any other rectangle, with the same center and sides parallel to the previous one, will also generate the same Voronoi diagram (Figure 21).
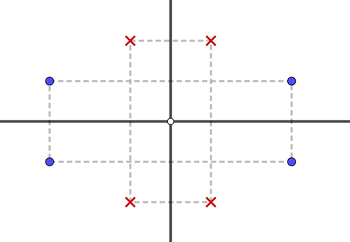
Figure 21: The vertices of both rectangles generate the same Voronoi diagram
This happens because the resulting Voronoi diagram node in the center of Figure 21 has an even degree (4 half-lines converge at it), which allows for symmetry in the composition of axial symmetries. This gives some flexibility to the position of the sites, see [4].
However, in practice, we can assume that all the nodes of our Voronoi diagrams have a degree of 3, which changes the situation completely. We will carry out the following reasoning for nodes of this degree, which are the ones we are interested in, but we can generalize it to any node of odd degree, see [2].
Consider a Voronoi diagram of at least four sites, with all its nodes having degree three. Let O and N be two extreme nodes of the same segment, and let A, B, and C be the sites whose circumcenter is O (so that A, B, and C are in general position, that is, not aligned), such that the segment ON lies on the median of A and B (Figure 22).
For another set of sites to generate the same diagram, they must be located in homothetic triangles with triangle ABC, with homothety center at O. If we now focus on a single Voronoi region, for example, the one corresponding to A, we observe that this forces any other site A' that generates the same region to be located on the half-line OA. (Obviously, once the position of A' on that half-line is fixed, the other two sites of the set are immediately determined, as they must be symmetrical to A' with respect to the edges converging at O).
Figure 22: The site A', an alternative to A, must be located on the half-line OA
Now, applying the same argument to node N, A' must also be located on the half-line NA. Therefore, A' must be the intersection of OA and NA: A' = A.
We then conclude that, given a Voronoi diagram corresponding to n point sites (n>3), with all its nodes having odd degree (that is, practically any Voronoi diagram), this set of n generating sites of the diagram is unique.
Transitioning from point sites to circular or polygonal shapes does not increase the freedom of the generating sites; rather, it reduces it. For example, a single median line can be generated by many different pairs of points, but a parabolic arc determines by itself the two objects it equidistantly separates, the focus and the directrix.
In summary, any of the Voronoi diagrams we have generated from the paintings determines the sensitive boundary of the silhouettes involved in its generation. As these silhouettes outline the focal areas of the positive space of the painting, the Voronoi diagram schematizes, in a single graph, a significant part of the distribution of the focal areas in the painting, thus contributing to improving our perception of form [12].
As a final reflection, we want to emphasize our desire for this work to contribute to highlighting the value, both educational and informative, that mathematical concepts and procedures acquire when applied in cultural contexts such as art, which are often (unjustly) accused of being cold or arid, but are also often (rightly) declared to be deeply emotional. We believe that a comprehensive education is one that fosters the appreciation of beauty in any of its forms, and ultimately, behind a painting or a theorem, we always find the same thing: human imagination.
Figure 21: The vertices of both rectangles generate the same Voronoi diagram
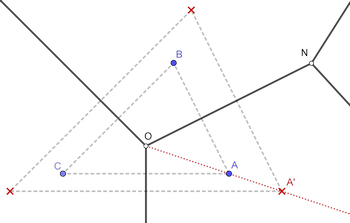
Figure 22: The site A', an alternative to A, must be located on the half-line OA