Berechnung von Rotationsvolumen
Rotation eines Funktionsgraphen - Rechtecknäherung
Und einmal mehr: die Rieman Streifen. Unten sehen Sie ein Bild unserer aus der Einführunf in die Integraechnung wohlbekannten Funktion. Die Fläche unter der Kurve ust durch Rechteckflächen angenähert. Stellen Sie sich nun vor dieser Funktionsgrapph würde um die x-Achse rotieren: a) Wie würden Sie den entstehenden Körper beschreiben? b) Welche Art Körper entsteht aus den Rechteckflächen? c) Geben Sie die Formel für die Grundfläche des aus den Rechteckflächen entstehenden Körpers an d) Geben Sie die Formel für das Volumen des aus den Rechteckflächen entstehenden Körpers an
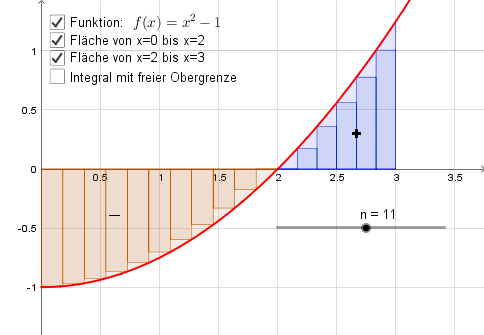
Der letzte kleine Schritt zur Volumenberenchnung
Damit steht die Methode zur Berechnung von Rotationsvolumina:
mal das Integral über das Quadrat der Funktion und die Sache ist geritzt! Einfluß des Verlaufs Oberhalb bzw. Unterhalb der x- Achse
Welche Auswirkungen auf das Volumen des entstehenden Rotationskörpers hat es, wenn die Funktion oberhalb oder wenn die Funktion unterhalb der x-Achse verläuft
Differenzen von Funktionen: Hohlräume in Körpern
Nun kann man auch Differenzkörper herstellen. In der Praxis geschieht das sehr oft: Beispielsweise bei der Herstellung von Drehteilen bei der Metallbearbeitung (z.B.: die Lagerschale eines Kugellagers).
Nehmen Sie die beiden Funktionen f und g in der Abbildung unten als Beispiel.
a) Beschreiben Sie den Rotationskörper, der im Intervall [2|6] entsteht. Haben Sie vielleicht ein Praxisbesipiel für solche Formen?
b) Wie muß man vorgehen, wenn das Volumen eines solchen Drehkörpers bestimmt werden soll?
c) Kann dies in der gleichen Weise geschehen, wie bei Schnittflächen von Funktionen?
