Distancia entre dos puntos
En el siguiente applet de GeoGebra, podrás corroborar el resultado de tus cálculos al utilizar la fórmula de "Distancia entre dos puntos". La posición de las coordenadas podrá modificarse desde la vista gráfica o algebraica.
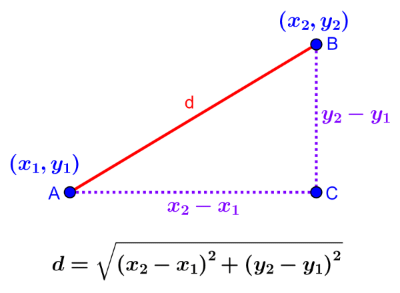
Para encontrar la distancia entre los puntos (A,B), es necesario aplicar el teorema de Pitágoras. El cual establece que: en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Generalizado lo anterior, se puede considerar que calcular la distancia entre dos puntos, equivale a determinar la longitud del segmento de recta cuyos extremos son dichos puntos. Si se representa el segmento en un plano cartesiano; y luego, en cada uno de sus extremos, se trazan rectas paralelas a los ejes cartesianos se forma un triángulo rectángulo cuya hipotenusa es el segmento del cual se desea medir su longitud.
1. Determina la distancia entre los puntos (1, 3) y (5, 6).
2. ¿Cuál es la distancia entre los puntos (2, 6) y (7, 10)?
3. Si es que tenemos los puntos (12, 2) y (5, 5), ¿cuál es su distancia?
4. Encuentra la distancia entre los puntos (-4, 5) y (4, 9).
5. Determina la distancia entre los puntos (-6, -7) y (-2, -1).