Množina bodov, z ktorých vidíme úsečku pod daným uhlom

Autor:: Beusiq

Množina bodov, z ktorých vidíme úsečku pod daným uhlom patrí k tzv. množine bodov roviny s danou vlastnosťou. Množinu všetkých bodov roviny s danou vlastnosťou označujeme ako G = {X є E2; V(X }, kde V(X) je charakteristická vlastnosť prvkov množiny G. Vlastnosť V je pre prvky množiny G charakteristická, ak platí : - každý prvok množiny G má vlastnosť V - každý prvok roviny, ktorý má vlastnosť V, je prvkom množiny G . Najčastejšími takýmito útvarmi sú : - Kružnica - Kruh - Os úsečky - Os uhla - Kuželosečka - Ekvidištančné priamky - Ekvidištančné kružnice - Množina bodov, z ktorých vidíme úsečku pod určitým uhlom Pozrime sa teraz bližšie na množinu bodov, z ktorých vidíme úsečku pod daným uhlom Množina bodov, z ktorých vidíme úsečku pod daným uhlom α je vlastne množina všetkých vrcholov uhlov s veľkosťou α v rovine, ktorých ramená prechádzajú bodmi A, B (A ≠ B). Je to množina všetkých bodov v rovine, z ktorých vidíme úsečku AB pod uhlom α. Ide vlastne o dva kružnicové oblúky k₁, k₂ s krajnými bodmi A, B ktoré ale do množiny G nepatria. Body, z ktorých sa javí nejaká úsečka pod daným uhlom, ležia na kružnicovom oblúku, čiže ide vlastne o obvodové uhly. Podľa veľkosti uhla α môžu nastať tri situácie :

[size=150][size=100]Ak je daný uhol menší, ako 90°, vykresľujeme vonkajšie kružnicové oblúky.
Ak je daný uhol väčší, ako 90°, no menší ako 180°, vykresľujeme vnútorné kružnicové oblúky.
Ak sa daný uhol rovná 90°, hovoríme o tzv. [i]Tálesovej kružnici[/i] - ak [i]AB[/i] je priemer kružnice, potom keď ľubovoľný iný bod [i]C[/i] kružnice spojíme bodmi [i]A[/i] a [i]B[/i], tak
spojnice budú zvierať pravý uhol a vznikne pravouhlý trojuholník [i]ABC[/i].
[i]Tálesova veta[/i] je vlastne špeciálnym prípadom vety o stredovom a obvodovom uhle. [/size][/size] — Ak je daný uhol menší, ako 90°, vykresľujeme vonkajšie kružnicové oblúky. Ak je daný uhol väčší, ako 90°, no menší ako 180°, vykresľujeme vnútorné kružnicové oblúky. Ak sa daný uhol rovná 90°, hovoríme o tzv. *Tálesovej kružnici* - ak AB je priemer kružnice, potom keď ľubovoľný iný bod C kružnice spojíme bodmi A a B, tak spojnice budú zvierať pravý uhol a vznikne pravouhlý trojuholník *ABC*. *Tálesova veta* je vlastne špeciálnym prípadom vety o stredovom a obvodovom uhle.

Predtým, než sa pustíme do rysovania takýchto kružnicových oblúkov si povedzme niečo o stredových a obvodových uhloch kružnice. Dva rôzne body na kružnici rozdelia kružnicu na dva kružnicové oblúky, jeden dlhší a druhý kratší - výnimkou je, ak spojnica bodov je priemerom kružnice. Spojením týchto dvoch bodov vznikne tetiva kružnice. Stredový uhol (ω) prislúchajúci k oblúku AB má vrchol v strede kružnice, jeho ramená prechádzajú koncovými bodmi oblúku a oblúk leží vo vnútri uhla. Obvodové uhly (α₁; α₂; α₃; …) prislúchajúce k oblúku AB majú vrcholy na opačnom, doplnkovom, oblúku. Ramená prechádzajú koncovými bodmi oblúka a oblúk leží vo vnútri uhla. Všetky obvodové uhly prislúchajúce k oblúku AB sú zhodné : α₁ = α₂ = α₃ = … = α Veta o obvodovom a stredovom uhle : V každej kružnici je stredový uhol dvojnásobkom ľubovoľného obvodového uhla prislúchajúceho tomu istému kružnicovému oblúku. Každé dva obvodové uhly prislúchajúce tomu istému kružnicovému oblúku sú zhodné. Obvodový uhol prislúchajúci menšiemu kružnicovému oblúku je ostrý a ten, ktorý prislúcha väčšiemu kružnicovému oblúku je tupý. Obvodový uhol prislúchajúci polkružnici je pravý uhol nad priemerom kružnice - Talesova veta. To, že veta o obvodom a stredovom uhle skutočne platí si dokážeme na troch rôznych prípadoch :

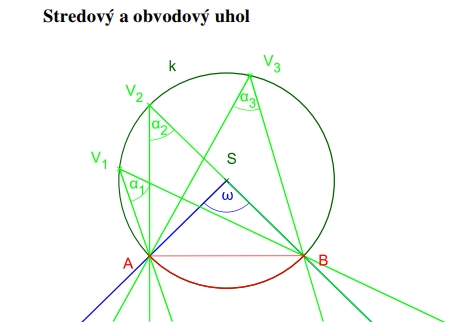
prípad 1

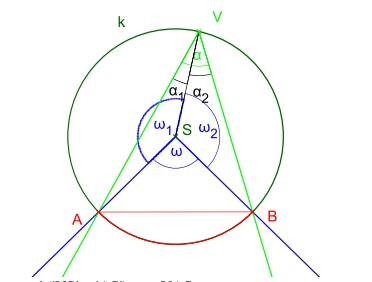
prípad 2

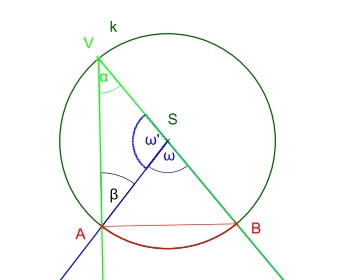
prípad 3

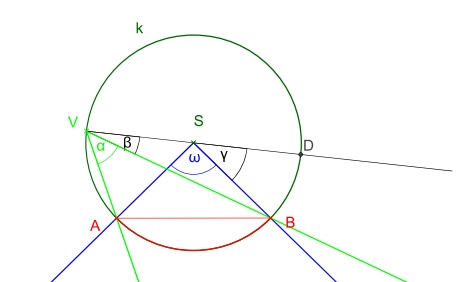
Postup konštrukcie množiny bodov, z ktorých vidíme úsečku pod daným uhlom

Máme danú úsečku AB a uhol α 1. Narysujeme os úsečky AB 2. Narysujeme polpriamku AQ, pričom uhol BAQ bude mať hodnotu α 3. Narysujeme priamku q, ktorá je kolmá na AQ a prechádza bodom A 4. Prienikom osi úsečky AB a priamky q získame bod S₁ 5. S₂ je stredovo súmerný s bodom S₁ podľa úsečky AB 6. Z bodov S₁, S₂zostrojíme kružnicové oblúky prechádzajúce bodmi A,B , zodpovedajúce zadanému uhlu α

[size=100]Pozrime sa trošku bližšie na uhly, ktoré sme dostali. Os úsečky [i]AB[/i] zviera s úsečkou [i]AB[/i] uhol 90° (os je na úsečku kolmá). Z bodu [i]A[/i] sme viedli polpriamku zvierajúcu s úsečkou [i]AB[/i] uhol [i]α [/i]a následne sme bodom [i]A[/i] viedli kolmicu na túto polpriamku. To znamená, že veľkosť uhla medzi kolmicou a úsečkou [i]AB[/i] je 90-[i]α. [/i]Uhol [i]AS[sub]1[/sub]B [/i]je stredovým uhlom kružnice [i]k [/i]vzhľadom k oblúku [i]AB [/i]a jeho veľkosť je [i]2α, [/i]z čoho vyplýva, že všetky obvodové uhly tohto oblúku vzhľadom ku kružnici [i]k[/i] budú mať veľkosť [i]α[/i] . [/size] — Pozrime sa trošku bližšie na uhly, ktoré sme dostali. Os úsečky AB zviera s úsečkou AB uhol 90° (os je na úsečku kolmá). Z bodu A sme viedli polpriamku zvierajúcu s úsečkou AB uhol α a následne sme bodom A viedli kolmicu na túto polpriamku. To znamená, že veľkosť uhla medzi kolmicou a úsečkou AB je 90-α. Uhol *AS₁B* je stredovým uhlom kružnice k vzhľadom k oblúku AB a jeho veľkosť je *2α,* z čoho vyplýva, že všetky obvodové uhly tohto oblúku vzhľadom ku kružnici k budú mať veľkosť α .

Príklad konštrukcie, kedy je daný uhol menší ako 90° - postup posúvajte tlačidlami

Príklad konštrukcie, kedy je daný uhol väčší ako 90°, no menší ako 180° - postup posúvajte tlačidlami

Príklad konštrukcie, kedy je daný uhol presne 90°, teda ide o Tálesovu kružnicu - postup posúvajte tlačidlami

Úloha s automatickým vyhodnotením : Presne stredom jazera v tvare kruhu vedie most. Pri jazera sú traja rybári. Dvaja sedia pri koncoch mosta a tretí niekde na brehu. Pod akým uhlom vidí rybár sediaci na brehu jazera most ?

Úloha s automatickým vyhodnotením : Daný je kosoštvorec ABCD. Zostrojte taký bod X, aby z neho bolo vidieť stranu AB pod uhlom 60° a stranu BC pod uhlom 45°.