Fungsi Kuadrat


1. Dapat menjelaskan bentuk umum fungsi kuadrat 2. Dapat mengidentifikasi sifat-sifat grafik fungsi kuadrat 3. Dapat menganalisis pengaruh nilai a, b, dan c 4. Dapat menentukan akar-akar fungsi kuadrat

![[justify][size=100]Pernahkah Anda mengamati lintasan bola basket saat Anda mendorong bola ke arah net? Lintasannya parabola dan gerak bola dikatakan parabola. Gambar tersebut menunjukkan posisi bola pada waktu tertentu. Bentuk parabola banyak ditemukan dalam kehidupan sehari-hari.
Parabola merupakan salah satu bentuk fungsi kuadrat dalam bentuk grafik. Fungsi kuadrat merupakan fungsi polinomial (banyak suku) dengan pangkat tertinggi variabelnya adalah 2. Anda masih ingat fungsi linear yang grafiknya berbentuk garis lurus. Fungsi linear merupakan fungsi polinomial dengan pangkat tertinggi variabelnya adalah 1.[/size][/justify]](https://www.geogebra.org/resource/twuz25sb/bfyH7MQ5aoOW4SOM/material-twuz25sb.png)
Pernahkah Anda mengamati lintasan bola basket saat Anda mendorong bola ke arah net? Lintasannya parabola dan gerak bola dikatakan parabola. Gambar tersebut menunjukkan posisi bola pada waktu tertentu. Bentuk parabola banyak ditemukan dalam kehidupan sehari-hari. Parabola merupakan salah satu bentuk fungsi kuadrat dalam bentuk grafik. Fungsi kuadrat merupakan fungsi polinomial (banyak suku) dengan pangkat tertinggi variabelnya adalah 2. Anda masih ingat fungsi linear yang grafiknya berbentuk garis lurus. Fungsi linear merupakan fungsi polinomial dengan pangkat tertinggi variabelnya adalah 1.


NAME:
CLASS:

Eksplorasilah alat GeoGebra yang disediakan dengan mengamati perubahan pada grafik fungsi kuadrat. Sesuaikan bilah dengan menggeser a, b, dan c untuk melihat bagaimana setiap nilai memengaruhi bentuk grafik. Perhatikan bagaimana perubahan nilai a memengaruhi lebar dan arah parabola, b menggeser titik puncak ke kiri atau kanan, dan c menentukan titik potong sumbu y. Selain itu, Anda dapat langsung memasukkan nilai untuk a, b, dan c untuk membuat grafik fungsi kuadrat sesuai keinginan. Melalui penjelajahan ini, Anda diharapkan memahami hubungan antara koefisien dalam persamaan kuadrat dan bentuk grafiknya.
Setelah menjelajahi GeoGebra untuk memahami pengaruh a, b, dan c pada fungsi kuadrat, jawablah pertanyaan di bawah ini.
NO.1
Apa yang terjadi pada bentuk grafik jika nilai a bertambah dan berkurang?
NO.2
Bagaimana perubahan nilai b memengaruhi posisi grafik fungsi kuadrat?
NO. 3
Jika hanya c yang diubah, bagaimana grafiknya akan berubah?
NO.4
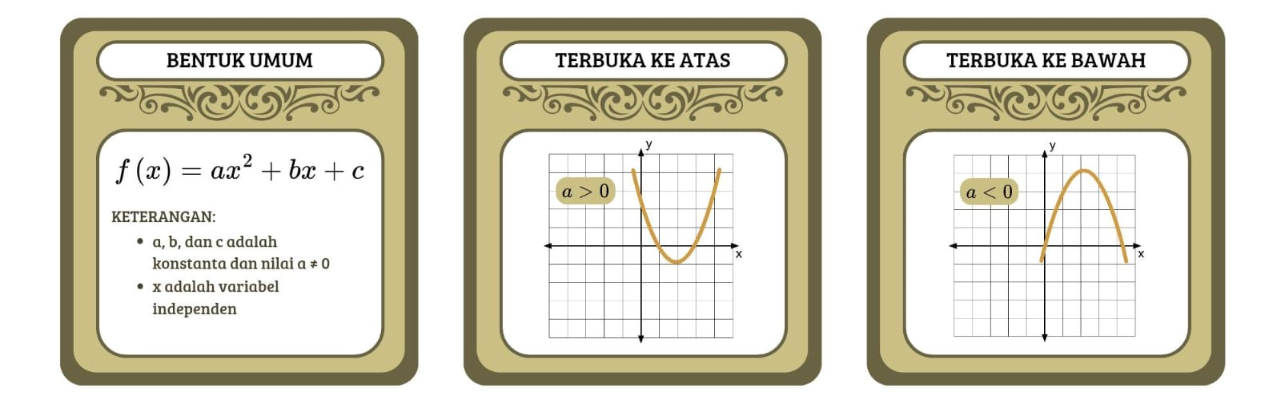
Jika a > 0, ke arah mana parabola terbuka? dan ke arah mana jika a < 0?
NO. 5
Coba ubah b menjadi nol. Apa yang terjadi pada simetri parabola?

ada tahap ini, Anda akan menjawab 10 pertanyaan dengan menyesuaikan poin yang tersedia. Langkah pertama adalah mencari akar persamaan menggunakan rumus yang telah dipelajari sebelumnya. Pada tool GeoGebra di bawah ini, terdapat tombol Start untuk memulai latihan. Setiap pertanyaan harus dijawab dengan benar, dan Anda dapat memeriksa jawaban Anda dengan mengklik tombol See Answer. Selain itu, tersedia bagian Score untuk menampilkan total poin yang telah Anda kumpulkan. Untuk menjawab, pindahkan kelima titik pada sistem koordinat Cartesian hingga sesuai dengan grafik fungsi kuadrat yang diberikan pada pertanyaan. Semoga berhasil!

Ayo Meringkas
Setelah mempelajari fungsi kuadrat, jelaskan bentuk umum fungsi kuadrat.
Ayo Meringkas
Uraikan sifat-sifat grafik, termasuk bentuk parabola, sumbu simetri, dan titik puncak.
Ayo Meringkas
nalisis pengaruh koefisien a, b, dan c pada grafik dan cara menentukan akar menggunakan diskriminan.
Ayo Meringkas
Terakhir, berikan contoh penerapan fungsi kuadrat dalam kehidupan sehari-hari.