Ebenengleichungen in Parameterform
Parameterform der Ebene
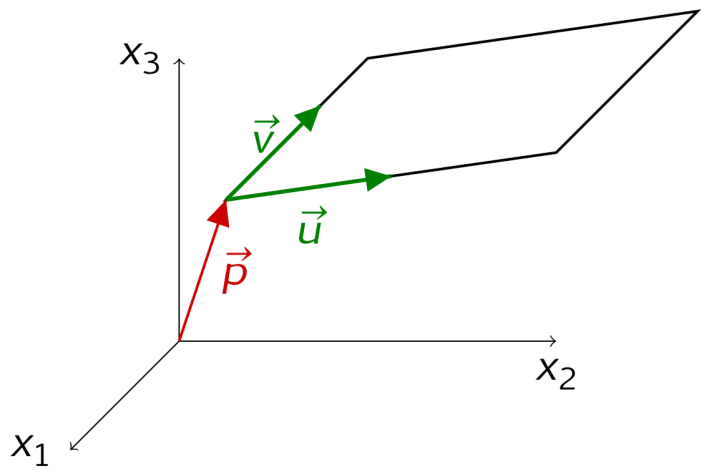
Für die Parameterform der Ebene benötigt man (ähnlich wie bei Geraden) einen Aufpunkt und zwei Richtungsvektoren sowie z Spurparameter.
Die Parameterform der Ebene
Erinnerst du dich noch, wie die Parameterform einer Gerade aufgebaut war? Ganz analog verhält es sich bei der Parameterform für die Ebene. Der einzige Unterschied: statt einen Richtungsvektor benötigt man nun 2 Richtungsvektoren und 2 Spurparameter.
Allgemein lässt sich eine Ebene also wie folgt darstellen: Jeder Punkt X ist eine Linearkombination aus einem Aufpunktvektor A und der Linearkombination aus zwei Richtungsvektoren v und w mit unabhängigen Spurparametern s und t. Es ist zu beachten, dass die beiden Vektoren v und w nicht kotlinear sein dürfen!
Video: Parameterform einer Ebene aufstellen
Erkunde! Die Parameterform für die Ebene
Hesse'sche Normalenform
Jetzt du!
Gib die Parameterform für die folgende Ebene an! Die Punkte A(1;0;0), B(0;3;0) und C(0;0;2) liegen auf der Ebene.